快速排序
快速排序是由东尼·霍尔所发展的一种排序算法。在平均状况下,排序 n 个项目要 Ο(nlogn) 次比较。在最坏状况下则需要 Ο(n2) 次比较,但这种状况并不常见。事实上,快速排序通常明显比其他 Ο(nlogn) 算法更快,因为它的内部循环(inner loop)可以在大部分的架构上很有效率地被实现出来。
快速排序使用分治法(Divide and conquer)策略来把一个串行(list)分为两个子串行(sub-lists)。
快速排序又是一种分而治之思想在排序算法上的典型应用。本质上来看,快速排序应该算是在冒泡排序基础上的递归分治法。
算法步骤
-
从数列中挑出一个元素,称为 “基准”(pivot);
-
重新排序数列,所有元素比基准值小的摆放在基准前面,所有元素比基准值大的摆在基准的后面(相同的数可以到任一边)。在这个分区退出之后,该基准就处于数列的中间位置。这个称为分区(partition)操作;
-
递归地(recursive)把小于基准值元素的子数列和大于基准值元素的子数列排序;
递归的最底部情形,是数列的大小是零或一,也就是永远都已经被排序好了。虽然一直递归下去,但是这个算法总会退出,因为在每次的迭代(iteration)中,它至少会把一个元素摆到它最后的位置去。
来源:https://github.com/hustcc/JS-Sorting-Algorithm
算法演示

排序动画过程解释
-
首先,操作数列中的所有数字
-
在所有数字中选择一个数字作为排序的基准(pivot), pivot 通常是随机选择的,在这里为了演示方便,我们选择最右边的数字作为 pivot
-
选取好 pivot 后,在操作数列中选择最左边的数字标记为 左标记 ,最右边的数字标记为 右标记
-
将左边的标记向右移动
-
当 左标记 达到超过 pivot 的数字时,停止移动
-
在这里,8 > 6 ,所以停止移动
-
然后将右边的标记向左移动
-
当 右标记 达到小于 pivot 的数字时,停止移动
-
在这里,4 < 6 ,所以停止移动
-
当左右标记停止时,更改标记的数字
-
因此,左标记 的作用是找到一个大于 pivot 的数字,右标记 的作用是找到一个小于 pivot 的数字
-
通过交换数字,可以在数列的左边收集小于 pivot 的数字集合,右边收集大于 pivot 的数字集合
-
交换之后,继续移动 左标记
-
在这里,9 > 6 ,所以停止移动
-
然后将右边的标记向左移动
-
当 右标记 碰撞到 左标记 时也停止移动
-
如果左右侧的标记停止时,并且都在同一个位置,将这个数字和 pivot 的数字交换
-
这就完成了第一次操作
-
小于 6 的都在 6 的左侧,大于 6 的都在 6 的右侧
-
然后递归对这分成的两部分都执行同样的操作
-
完成 快速排序
代码实现
为了更好的让读者用自己熟悉的编程语言来理解动画,笔者将贴出多种编程语言的参考代码,代码全部来源于网上。
C++代码实现

Java代码实现
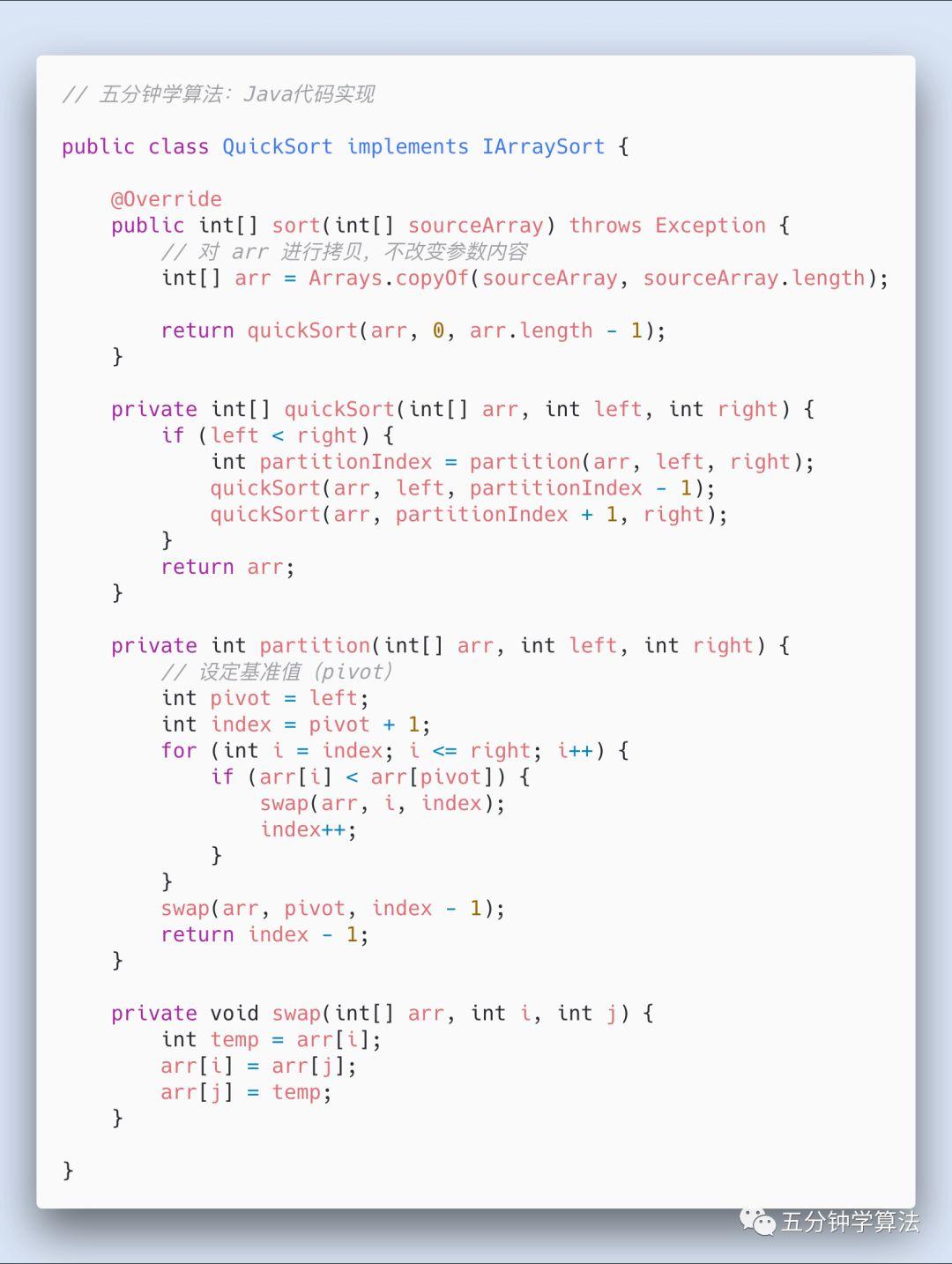
Python代码实现

JavaScript代码实现
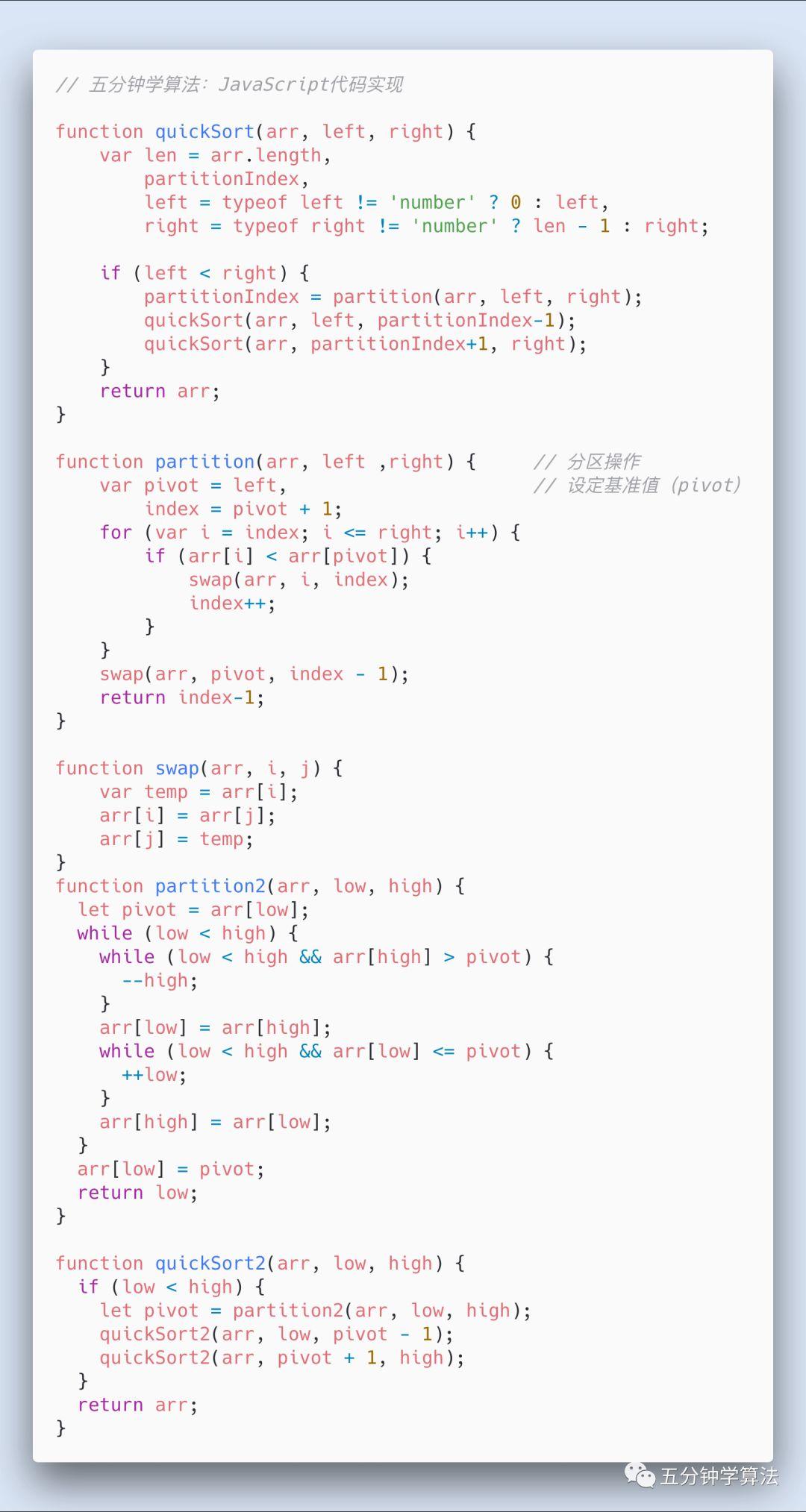
如果你是iOS开发者,可以在GitHub上 https://github.com/MisterBooo/Play-With-Sort-OC 获取更直观可调试运行的源码。
如果你想获取高清的动画演示,在 五分钟学算法 公众号里回复 快速排序 即可。
五分钟学算法


长按识别二维码关注:为您提供更多算法动画解析





