作者:李威
中文地址:https://leetcode-cn.com/problems/permutations-ii/
英文地址:https://leetcode.com/problems/permutations-ii/
我写的题解地址:https://leetcode-cn.com/problems/permutations-ii/solution/hui-su-suan-fa-python-dai-ma-java-dai-ma-by-liwe-2/
思路分析:
这一题是在 「力扣」第 46 题:“全排列” 的基础上增加了“序列中的元素可重复”这一条件。因此我们还使用“回溯”算法,只不过在构建递归树的过程中需要“剪枝”,以去除重复元素。
因为“序列中的元素可重复”,所以得到的“全排列”就会出现重复的结果,因此我们需要想办法把重复的“全排列”去掉。
如何去重
1、发现困难
这道题我们完全可以按照第 46 题,在结果集中去重,不过在实际编码的时候,我们发现并不好做:如果是简单的数字,直接放在哈希表中去重就好了,但这道题可能产生重复的是一个列表对象。
2、在以前做过的问题中寻找经验
去重复的一个经验是:在一个数组中去掉重复元素,除了使用哈希表,还有一种办法是将原始数组排序(升序、降序均可)。排序以后,重复的元素一定不会是数组第 0 号索引位置的元素。因为相同元素只保留 1 个,我们保留第 1 个或者保留最后 1 个是相对容易编码的。
「力扣」第 15 题:“三数之和” 就利用这样的思路,在遍历到相同元素的第 2 个的时候,将当前循环 continue 掉,这一步也可以认为是“剪枝”操作。放在这一题也是一样的,同样的思路还可以应用于第 39 题、第 40 题、第 78 题、第 90 题。
下面我具体解释一下这个思想应用于本题的过程。在第 46 题中,如果没有重复元素画出的树形图是这样的。
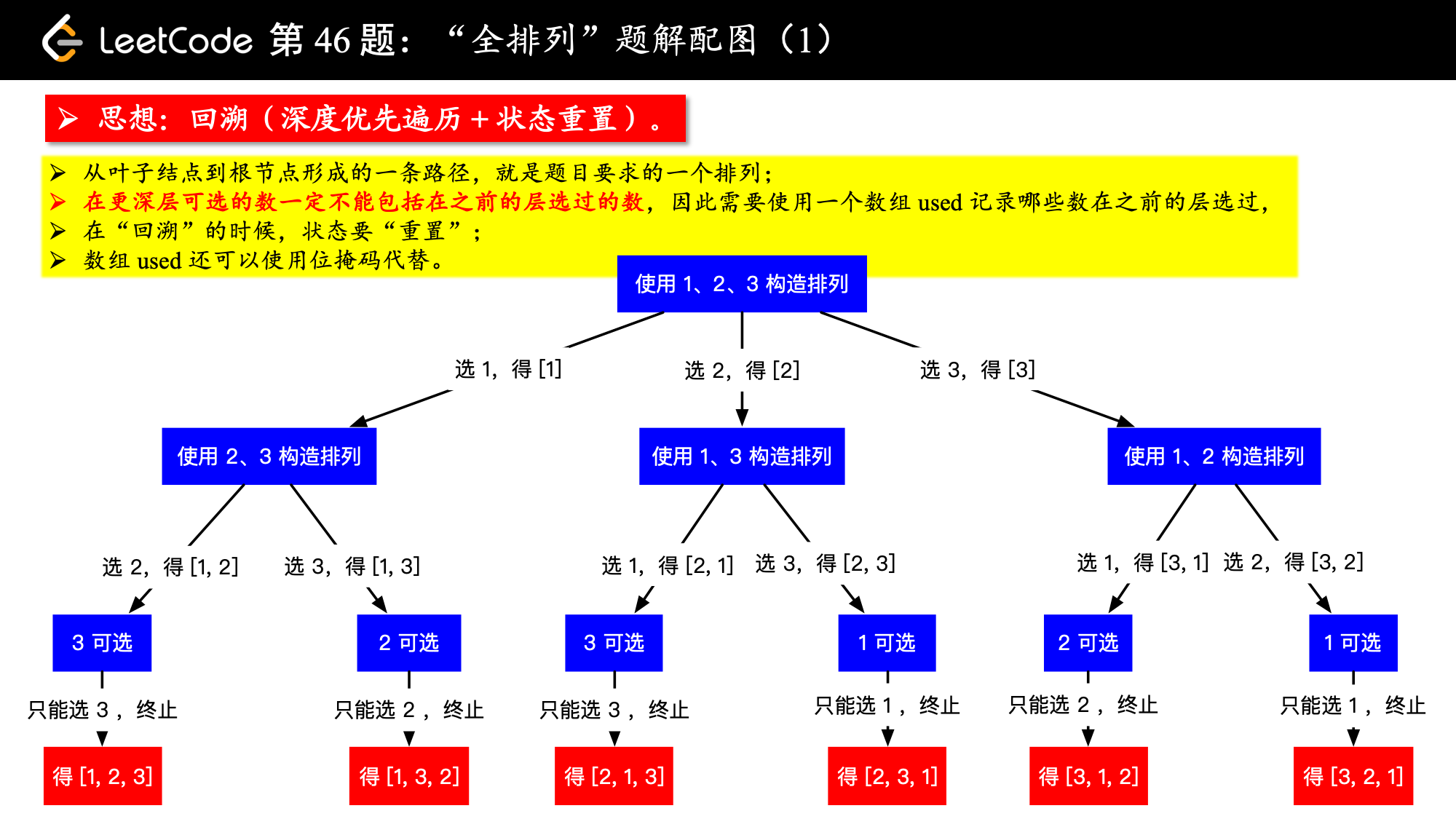
46-1.png
下面的描述基于我为「力扣」第 46 题:“全排列”编写的题解 《回溯算法(Python 代码、Java 代码) 。
方法:回溯 + 剪枝(剪枝的效果是“去重复”)
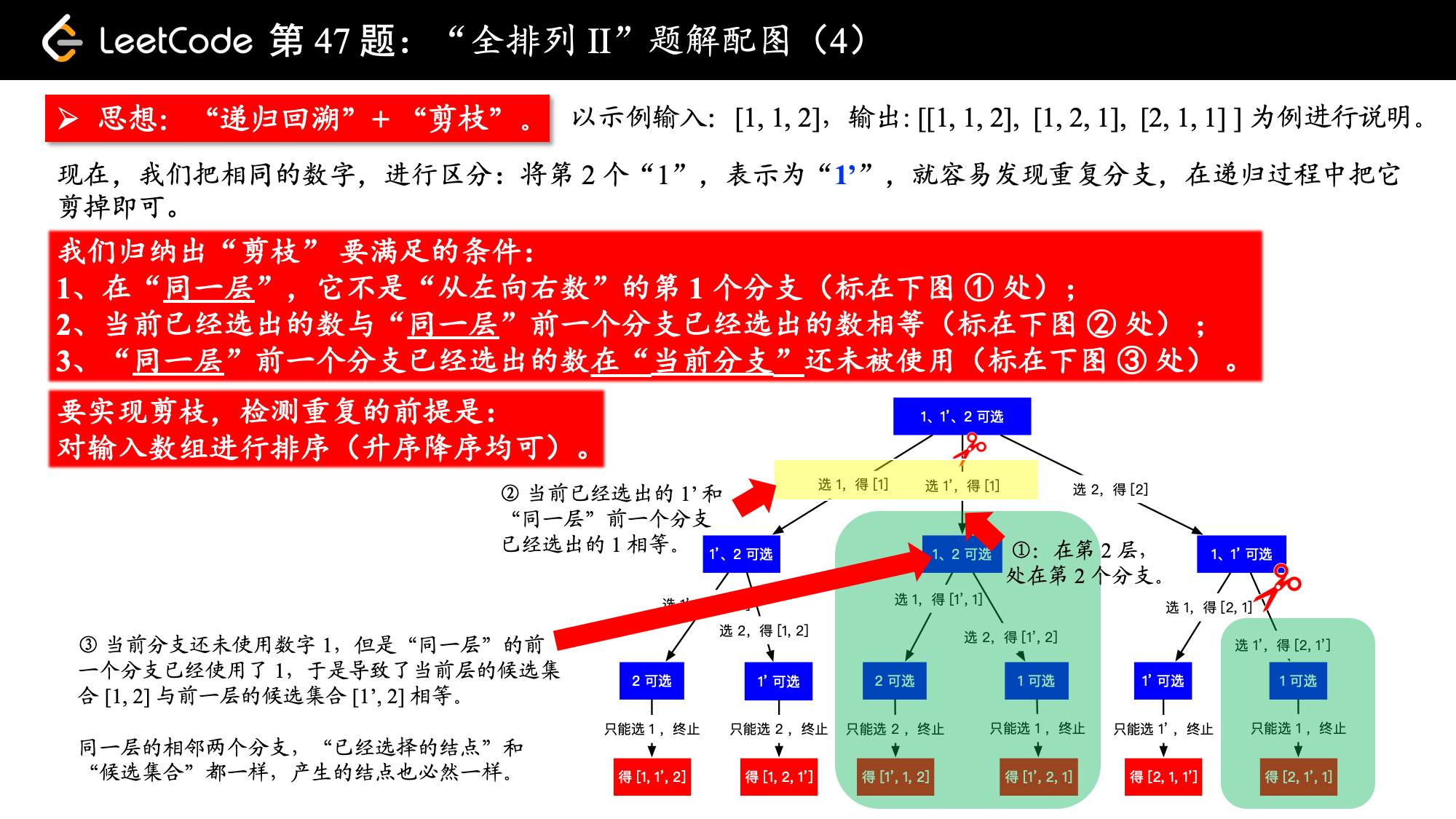
下面这段话是解决有重复元素的序列的排列问题的关键:当数组中有重复元素的时候,可以先将数组排序,排序以后在递归的过程中可以很容易发现重复的元素。当发现重复元素的时候,让这一个分支跳过,不再继续搜索,以达到“剪枝”的效果,重复的排列就不会出现在结果集中。
请看下图,我们把排序以后的数组,就当做它没有重复元素的话,还按照之前的回溯方法,也很容易看出重复的分支,把它剪去即可。
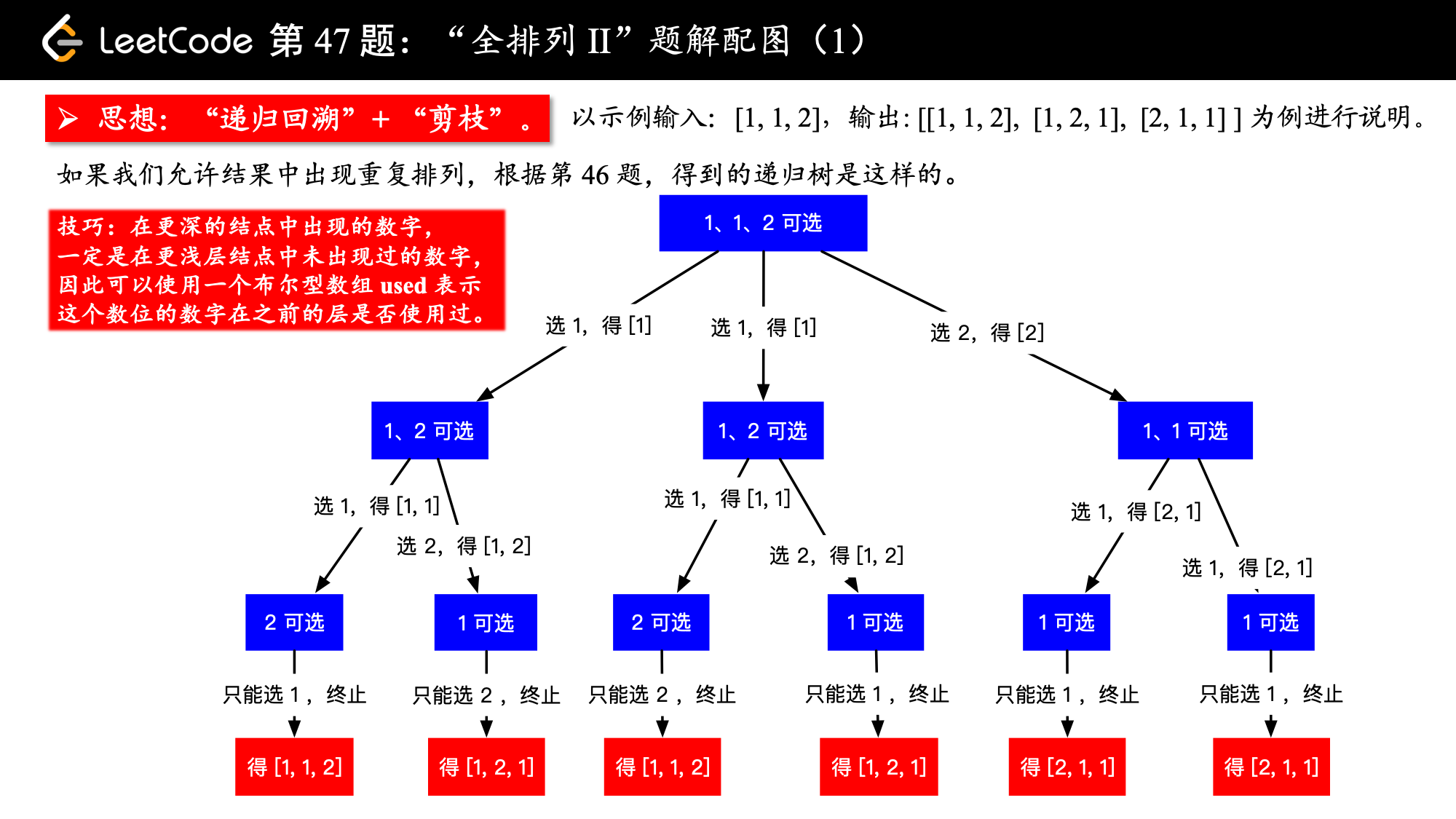
47-1.png
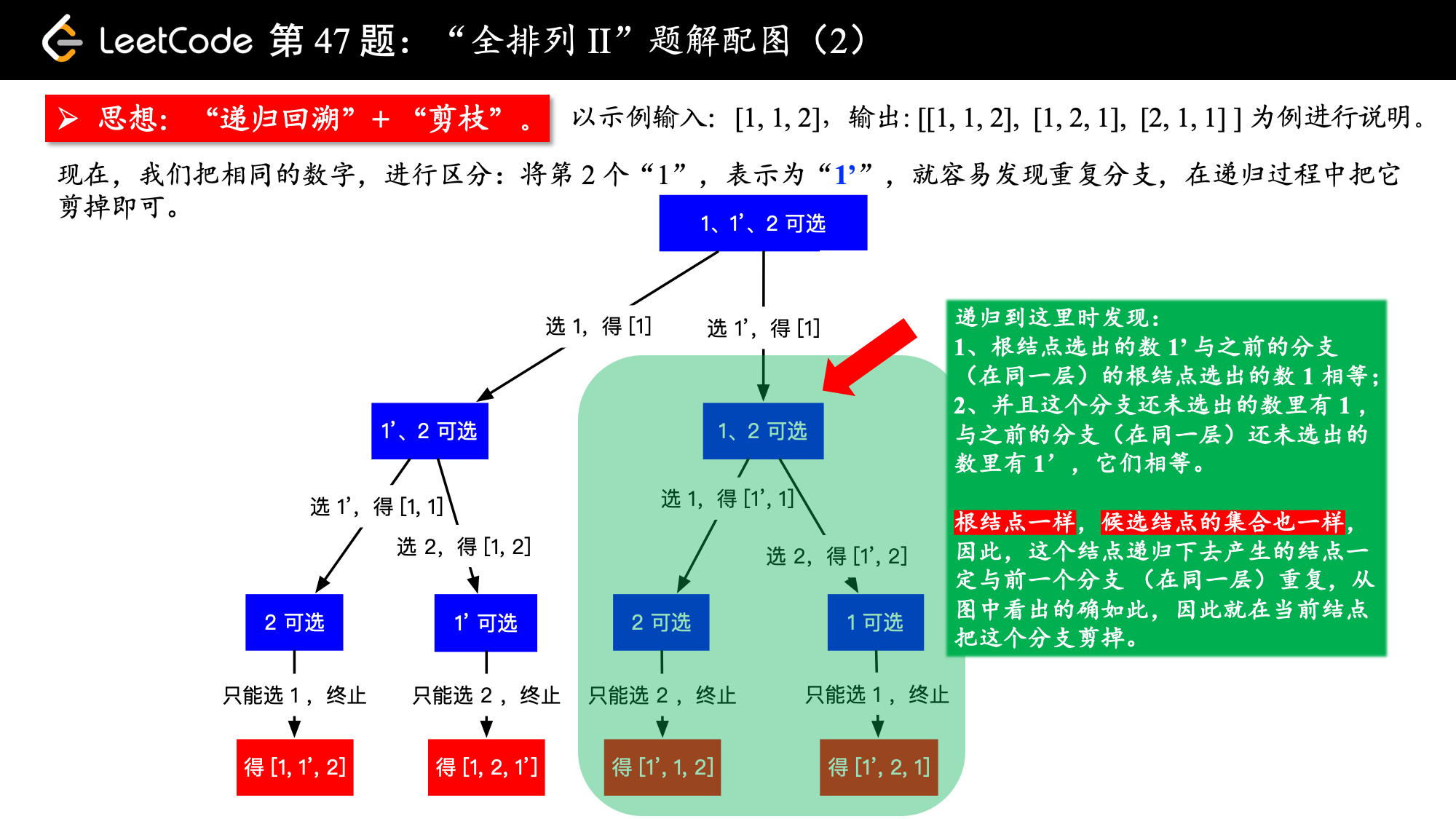
47-2.png
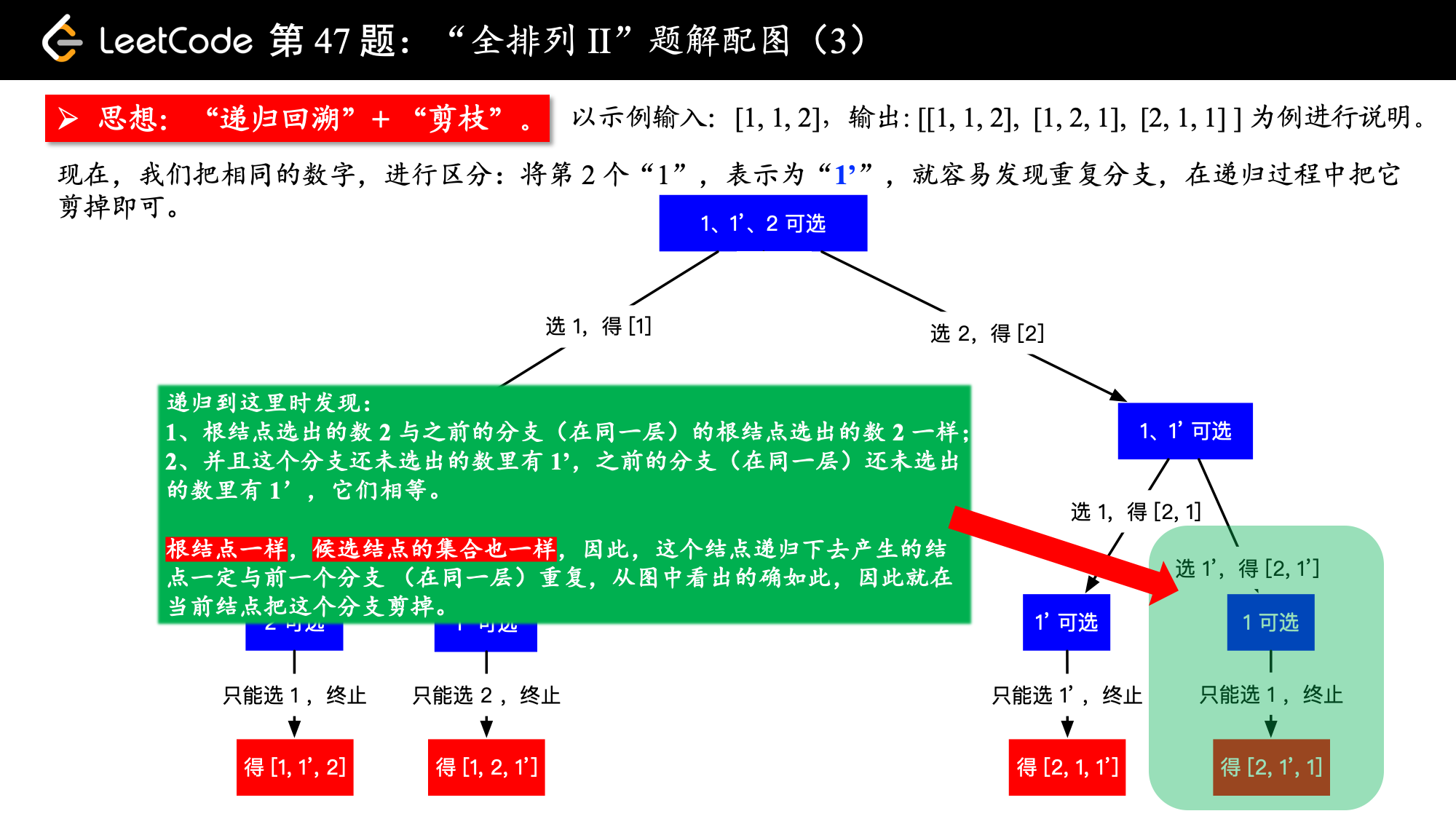
47-3.png
47-4.png
说明:
下面这个代码片段:
if (i > 0 && nums[i] == nums[i - 1] && !used[i - 1]) {
continue;
}
中的 used[i - 1] 加或者不加 ! ,提交到力扣的代码测评系统中都是可以通过的,下面我解释一下原因。
以 [2, 3, 3, 3] 中的 3 个 3 为例,相同的 3 个 3 有 6 个排列。我们只要保留 1 个就好了。
它们的索引分列是:
[1, 2, 3](数组中的数组表示 3 这个元素在[2, 3, 3, 3]这个数组中的索引,在全排列中可能的“排列”,下同)[1, 3, 2][2, 1, 3][2, 3, 1][3, 1, 2][3, 2, 1]
发现其实又是一个全排列问题。首先联系数组 used[i - 1] 的语义:used[i - 1] == true 表示索引 i 位置的前一个位置元素已经使用过。在 used[i - 1] == true 的时候全部 continue 掉,则只剩下了 used[i - 1] == false 的情况,即当前遍历的元素的之前的元素均未使用过,因此保留了 [3, 2, 1] 这种排列。
反之理解另一种情况。
下面用一个具体的例子来说明:
1、如果剪枝写的是:
if (i > 0 && nums[i] == nums[i - 1] && !used[i - 1]) {
continue;
}
那么,对于数组 [1, 1’, 1’’, 2],回溯的过程如下:
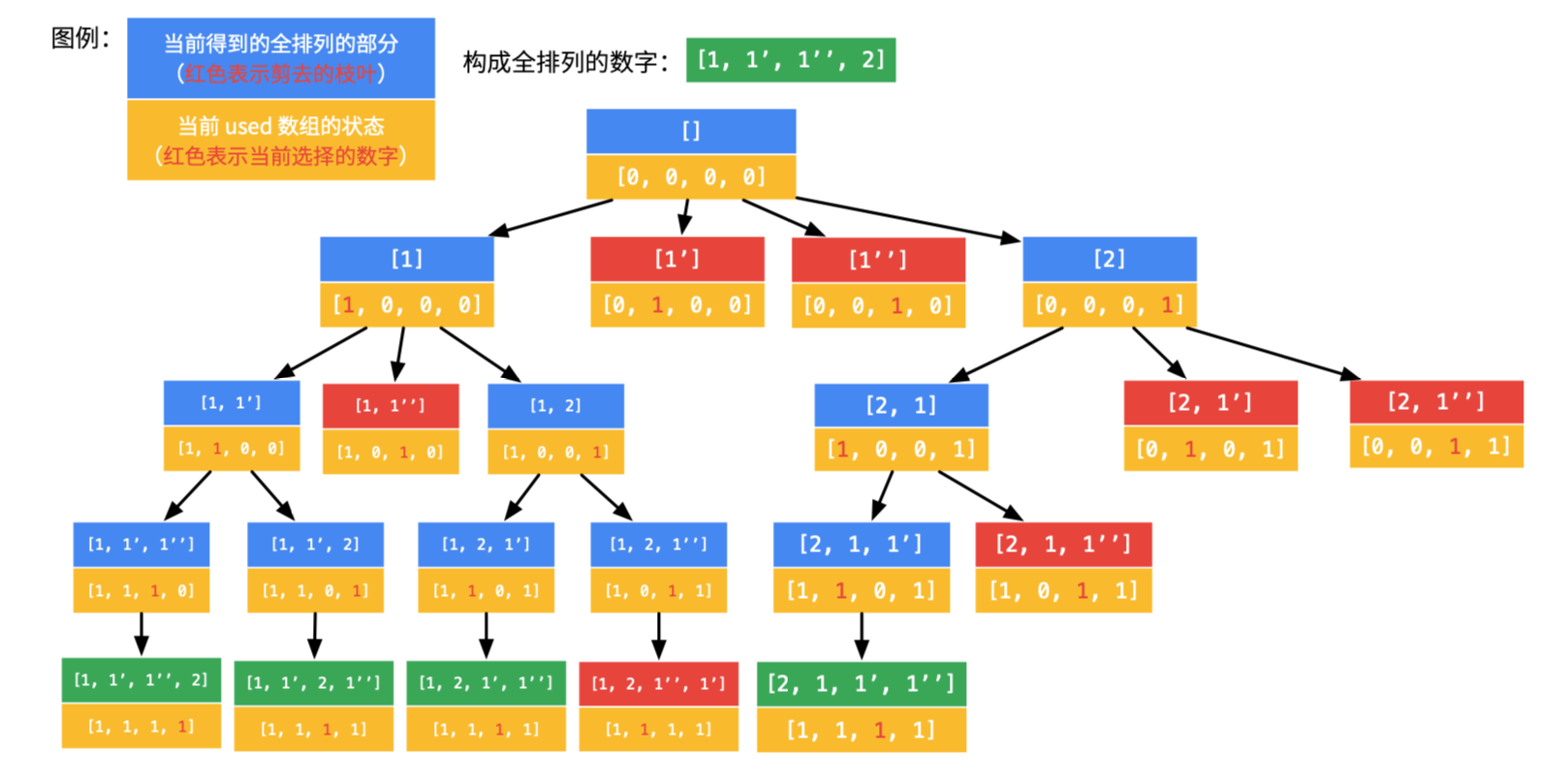
得到的全排列是:[[1, 1', 1'', 2], [1, 1', 2, 1''], [1, 2, 1', 1''], [2, 1, 1', 1'']]。特点是:1、1'、1'' 出现的顺序只能是 1、1'、1''。
2、如果剪枝写的是:
if (i > 0 && nums[i] == nums[i - 1] && used[i - 1]) {
continue;
}
那么,对于数组 [1, 1’, 1’’, 2],回溯的过程如下(因为过程稍显繁琐,所以没有画在一张图里):
1、先选第 1 个数字,有 4 种取法;
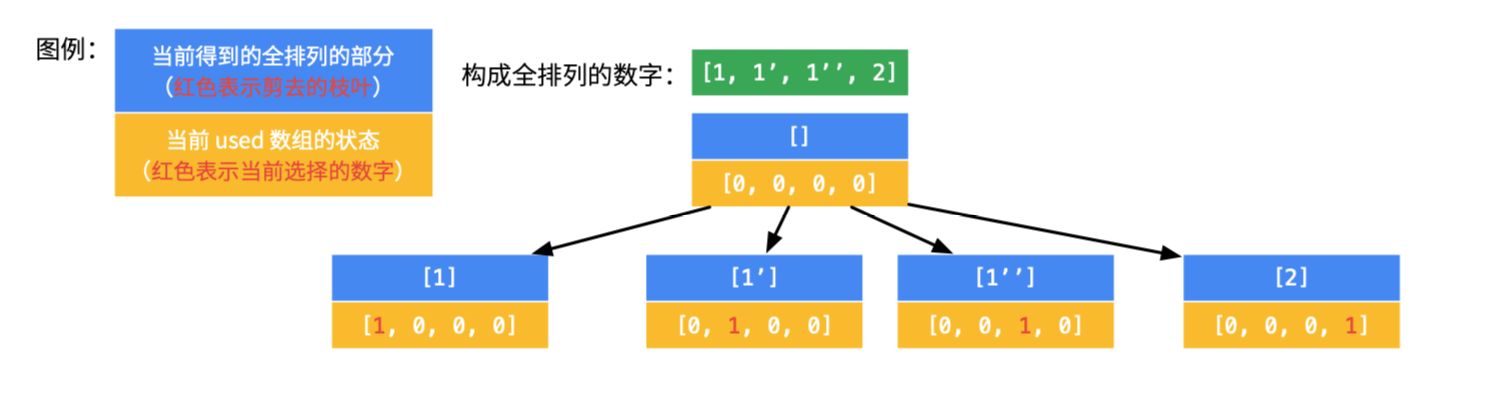
2、对第 1 步的第 1 个分支,可以继续搜索,但是发现,没有搜索到合适的叶子结点;
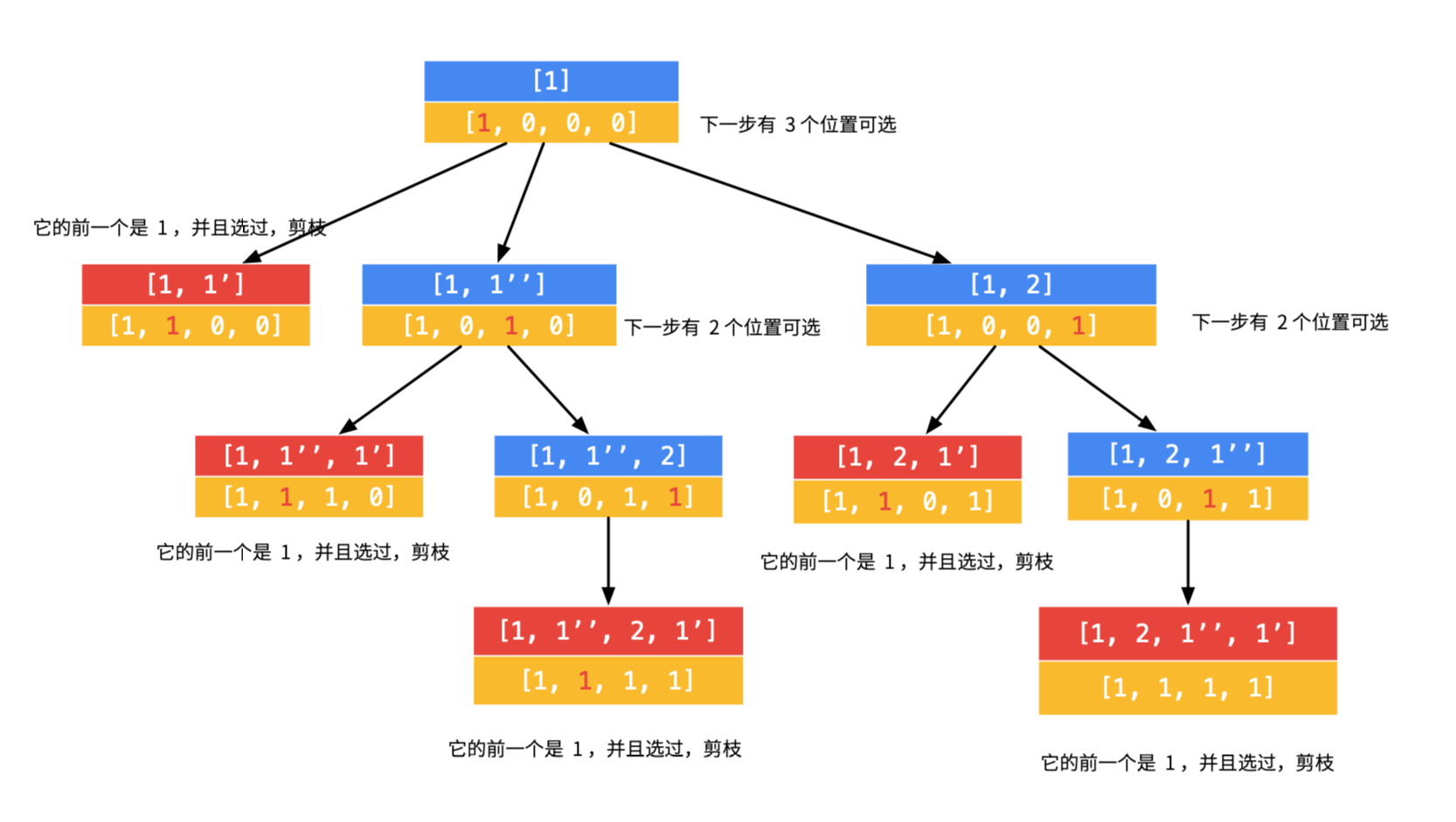
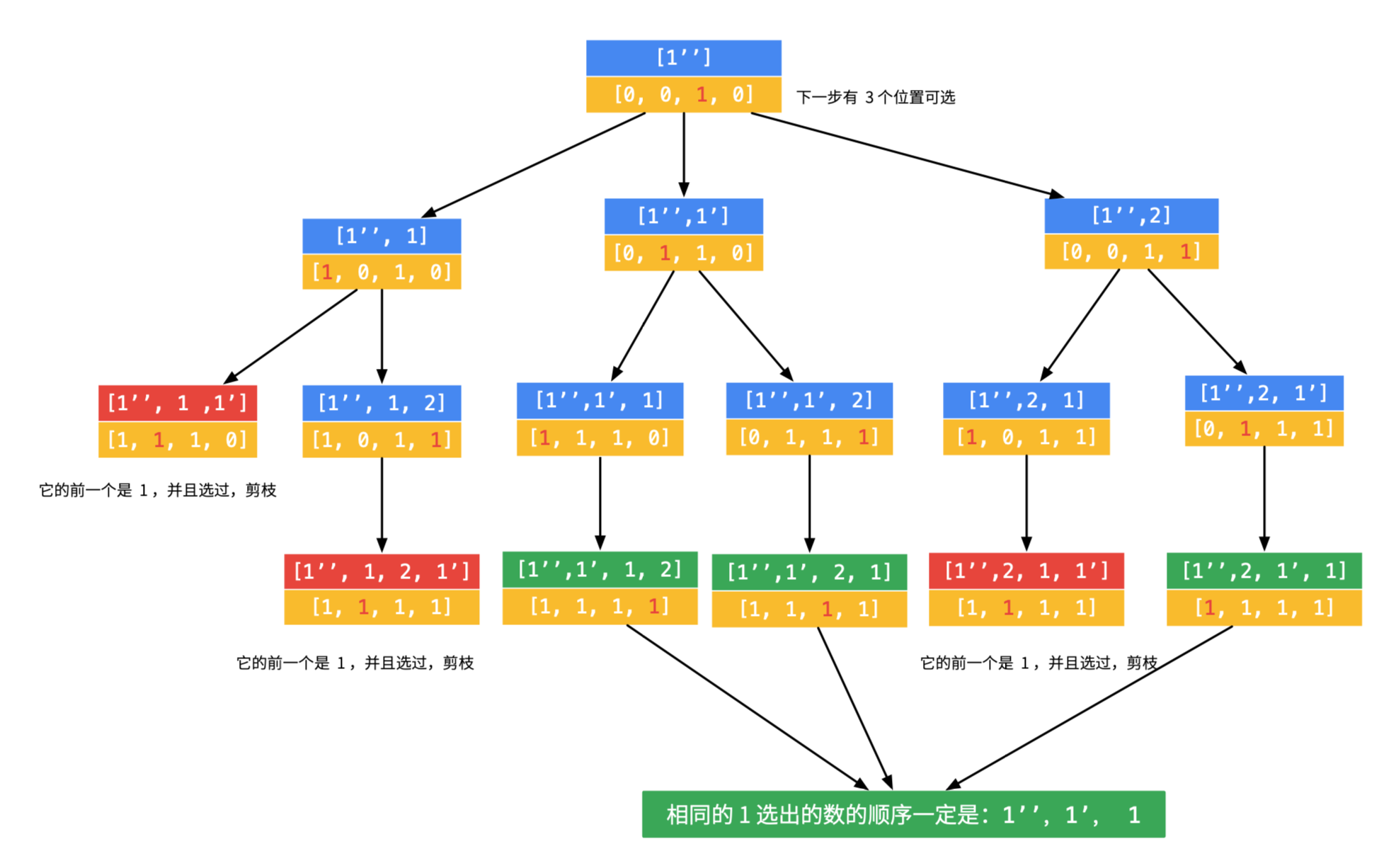
3、对第 1 步的第 2 个分支,可以继续搜索,但是同样发现,没有搜索到合适的叶子结点;
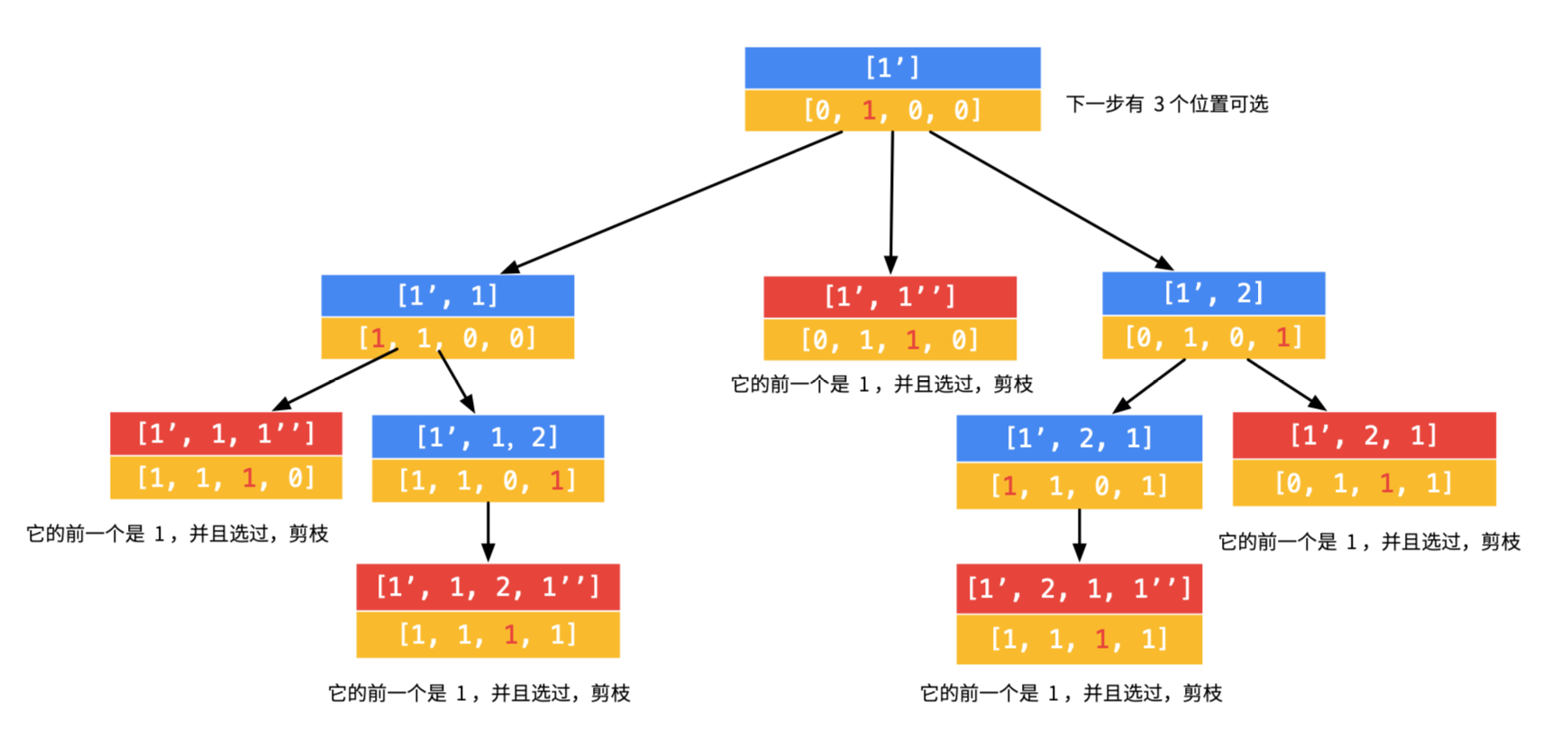
4、对第 1 步的第 3 个分支,继续搜索发现搜索到合适的叶子结点;
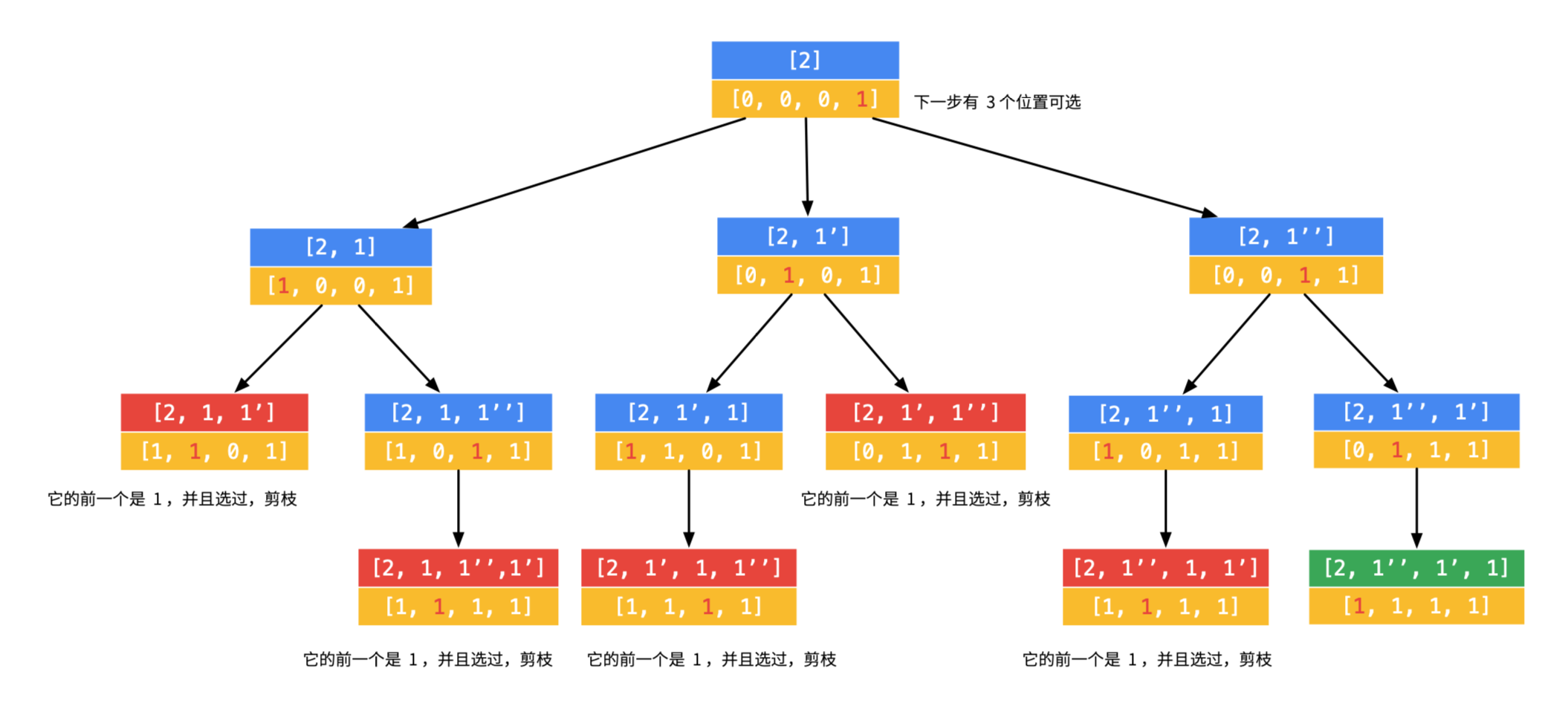
5、对第 1 步的第 4 个分支,继续搜索发现搜索到合适的叶子结点;
因此,used[i - 1] 前面加不加感叹号的区别仅在于保留的是相同元素的顺序索引,还是倒序索引;应用于本题,则是相同分支保留的是第 1 个分支还是最后一个分支,它们在结果集中是“等价的”,具体加感叹号对应哪种情况,不加感叹号,对应哪种情况,我个人觉得并不太重要。
以下代码根据我在「力扣」第 46 题:全排列 II 中的题解(上文有给出链接)中的示例代码修改而来,具体修改的地方,在下面代码的注释中有说明。
基于第 46 题,做 2 处修改即可:
1、在开始回溯算法之前,对数组进行一次排序操作,这是上面多次提到的;
2、在进入一个新的分支之前,看一看这个数是不是和之前的数一样,如果这个数和之前的数一样,并且之前的数还未使用过,那接下来如果走这个分支,就会使用到之前那个和当前一样的数,就会发生重复,此时分支和之前的分支一模一样。(这句话特别关键,可以停下来多看两遍,再看一看上面画的那张图)。
参考代码:(感谢用户 @carryzz 提供的 C++ 代码)
C++ 代码:
// author: carryzz
#include <iostream>
#include <vector>
using namespace std;
class Solution {
public:
vector<vector<int>> permuteUnique(vector<int> &nums) {
sort(nums.begin(), nums.end());
int n = nums.size();
vector<int> temp;
vector<vector<int>> res;
vector<bool> visited(n, false);
DFS(nums, temp, res, 0, visited);
return res;
}
void DFS(vector<int> &nums, vector<int> &temp, vector<vector<int>> &res, int cursize, vector<bool> &visited) {
if (cursize == nums.size()) {
res.push_back(temp);
return;
}
for (int i = 0; i < nums.size(); i++) {
if (!visited[i]) {
if (i > 0 && nums[i] == nums[i - 1] && !visited[i - 1])
continue;
temp.push_back(nums[i]);
visited[i] = true;
DFS(nums, temp, res, cursize + 1, visited);
temp.pop_back();
visited[i] = false;
}
}
}
};
int main() {
Solution solution = Solution();
vector<int> nums;
nums.push_back(2);
nums.push_back(3);
nums.push_back(3);
vector<vector<int>> res = solution.permuteUnique(nums);
// 使用索引遍历
int i, j;
cout << "Use index : " << endl;
for (i = 0; i < res.size(); i++) {
for (j = 0; j < res[0].size(); j++)
cout << res[i][j] << " ";
cout << endl;
}
// 使用迭代器遍历
vector<int>::iterator it;
vector<vector<int>>::iterator iter;
vector<int> vec_tmp;
cout << "Use iterator : " << endl;
for (iter = res.begin(); iter != res.end(); iter++) {
vec_tmp = *iter;
for (it = vec_tmp.begin(); it != vec_tmp.end(); it++)
cout << *it << " ";
cout << endl;
}
return 0;
}
Java 代码:
import java.util.ArrayList;
import java.util.Arrays;
import java.util.Collections;
import java.util.List;
import java.util.Stack;
import java.util.stream.Collectors;
import java.util.stream.IntStream;
public class Solution {
private List<List<Integer>> res = new ArrayList<>();
private boolean[] used;
private void findPermuteUnique(int[] nums, int depth, Stack<Integer> stack) {
if (depth == nums.length) {
res.add(new ArrayList<>(stack));
return;
}
for (int i = 0; i < nums.length; i++) {
if (!used[i]) {
// 修改 2:因为排序以后重复的数一定不会出现在开始,故 i > 0
// 和之前的数相等,并且之前的数还未使用过,只有出现这种情况,才会出现相同分支
// 这种情况跳过即可
if (i > 0 && nums[i] == nums[i - 1] && !used[i - 1]) {
continue;
}
used[i] = true;
stack.add(nums[i]);
findPermuteUnique(nums, depth + 1, stack);
stack.pop();
used[i] = false;
}
}
}
public List<List<Integer>> permuteUnique(int[] nums) {
int len = nums.length;
if (len == 0) {
return res;
}
// 修改 1:首先排序,之后才有可能发现重复分支
Arrays.sort(nums);
// 如果是降序,需要把 nums 变为包装数组类型,输入 Arrays.sort() 方法才生效,并且还要传入一个比较器,搜索之前,再转为基本类型数组,因此不建议降序排序
// Integer[] numsBoxed = IntStream.of(nums).boxed().collect(Collectors.toList()).toArray(new Integer[0]);
// Arrays.sort(numsBoxed, Collections.reverseOrder());
// nums = Arrays.stream(numsBoxed).mapToInt(Integer::valueOf).toArray();
used = new boolean[len];
findPermuteUnique(nums, 0, new Stack<>());
return res;
}
}
Python 代码:
class Solution:
def permuteUnique(self, nums):
if len(nums) == 0:
return []
# 修改 1:首先排序,之后才有可能发现重复分支,升序、倒序均可
nums.sort()
# nums.sort(reverse=True)
used = [False] * len(nums)
res = []
self.__dfs(nums, 0, [], used, res)
return res
def __dfs(self, nums, index, pre, used, res):
if index == len(nums):
res.append(pre.copy())
return
for i in range(len(nums)):
if not used[i]:
# 修改 2:因为排序以后重复的数一定不会出现在开始,故 i > 0
# 和之前的数相等,并且之前的数还未使用过,只有出现这种情况,才会出现相同分支
# 这种情况跳过即可
if i > 0 and nums[i] == nums[i - 1] and not used[i - 1]:
continue
used[i] = True
pre.append(nums[i])
self.__dfs(nums, index + 1, pre, used, res)
used[i] = False
pre.pop()





