
在《算法导论》第二版第 7 章(快速排序)的思考题(第 95 页)中提及到一种 低效的递归排序算法:Stooge 排序, Howard、Fine 等教授将这个算法称为 漂亮排序算法(完美排序算法)。
经过证明,Stooge 排序的性能是慢于冒泡排序的,因为这个,在《算法导论》中作者悄悄的 “diss” 了一下这几位终生教授,“怀疑”他们是否“名副其实”。
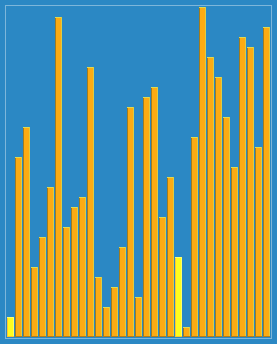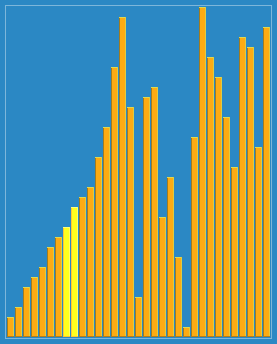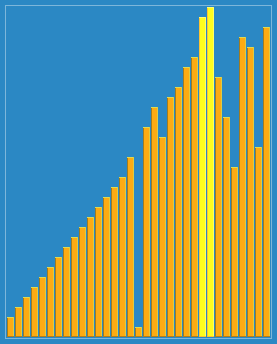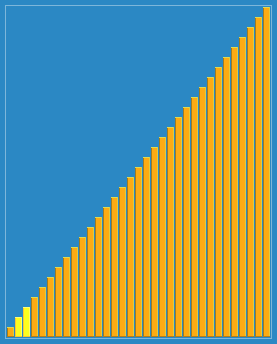
顾名思义, 漂亮排序算法 它的代码实现 看、上、去 很整齐很好看!
//@程序员小吴 在《算法导论》第 2 版第 95 页,里面使用的是 i 和 j,为了
//更好理解,我在这里使用了 low 和 high 进行代替
private static void stoogeSort(int[] A, int low, int high){
if(A[low] > A[high]) swap(A, low, high);
if(low + 1 >= high ) return;
int split = (high - low + 1) / 3;
stoogeSort(A, low, high - split);
stoogeSort(A, low + split, high);
stoogeSort(A, low, high - split);
}
通过图片你可能更能直观的看出它的好看。

代码整体的思路就是基于递归来实现的,具体操作就是:对于传入的数组先将头部与尾部进行排序,然后递归调用排序前三分之二,再递归调用排序后三分之二,最后再递归调用排序前三分之二。
动画描述
1.第一步:对传入的数组的头尾元素进行比较

2.第二步:判断能否三等分,如果可以则将数组三等分

3.第三步:同样的逻辑递归的排序数组的前 2 / 3 区域

4.第四步:同样的逻辑递归的排序数组的后 2 / 3 区域
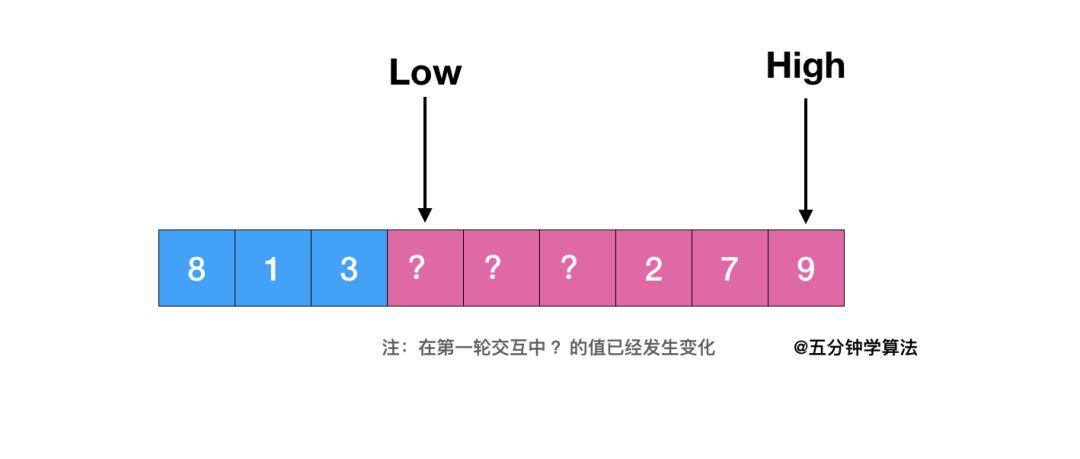
5.第五步:同样的逻辑再次递归的排序数组的前 2 / 3 区域
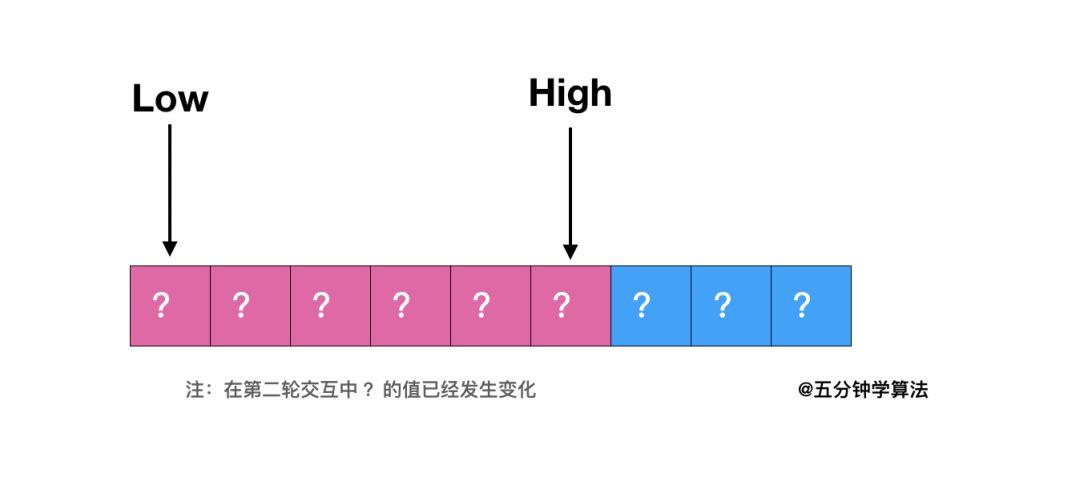
排序完成!
这个算法的复杂度为 T(n) = 3 T( 2n / 3 ) + 1,已被其它大牛证明时间复杂度接近于 O(n2.71) ,对比于一般的排序算法,比如冒泡、选择等常见的 O(n2) 排序算法,排序过程上慢很多。
所以,它除了好看,目前也没发现有啥用:一顿操作瞎装逼,一看性能二点七!
再补充一个有趣的点,这个算法也被称之为 臭皮匠算法: 三个臭皮匠顶个诸葛亮(在代码实现中涉及到三等分这个概念)。
如果你对这种奇葩排序感兴趣的话,不妨点击下面两个链接看看,涉及到猴子排序、面条排序、鸡尾酒排序等各种奇葩排序的动画描述。
你还知道哪些奇葩算法?欢迎留言告诉小吴。






