在计算机领域离不开算法和数据结构,而在数据结构中我们往往需要一些灵巧的结构去处理一些繁杂的数据,链表 就是这样一种能穿针引线般的帮助我们去解决这种问题的数据结构。
它可以辅助组成其他数据结构比如 队列 。
后续的比如二分搜索树,平衡二叉树,红黑树等动态数据结构都可以在理解链表的基础上进行深入的学习。
如果你是一个计算机初学者,那么对于链表的学习可以帮助你理解 递归 ,因为后续的二叉树中需要深入理解 递归 。
链表的定义
在《算法(第4版)》中,对链表的定义如下:
链表是一种递归的数据结构,它或者为空(null),或者是指向一个结点(node)的引用,该节点还有一个元素和一个指向另一条链表的引用。
链表的数据存储在“节点”(Node)中:

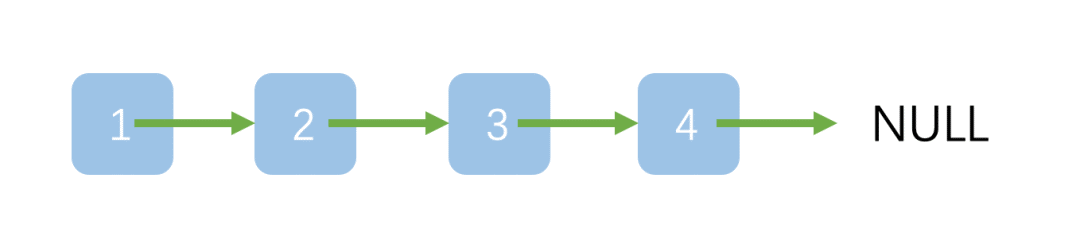
在上节的 栈与队列 一文中,都提到了 resize 这个操作,而通过观察链表的数据结构可以发现:
-
最后一个节点的 next 指向 NULL ,这个节点是最后一个节点
-
不像数组一下子必须new出来一片空间,无需考虑空间不够用或浪费
-
需要多少个数据,就能生成多少个节点挂接起来
也就是说:链表具有动态的能力,不需要去处理固定容量的问题。
正因为链表具备这种动态能力,那它也就缺失了高效的random access(随机访问)的能力。它无法与数组一样,通过一个索引(index)直接获取对应的元素。
因为在底层机制中数组开辟的空间在内存中是连续分布的,我们可以直接寻找索引对应的偏移,直接计算出数据所存储的内存地址,直接用O(1)复杂度拿出。
链表靠next连接,每个节点存储地址不同,我们只能通过next顺藤摸瓜找到我们要找的元素。
链表的实现

这些就是链表的成员变量以及常用方法。
链表的添加元素操作
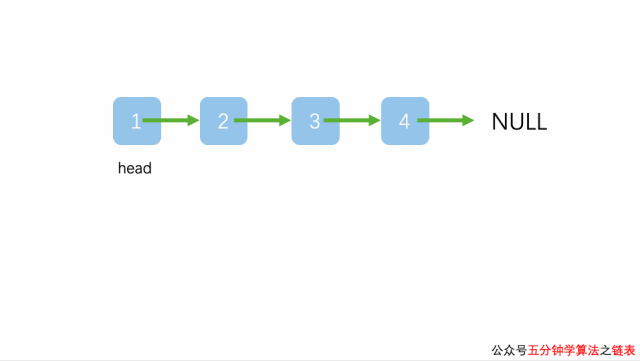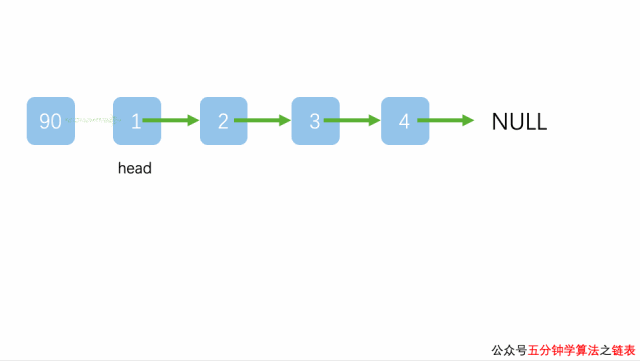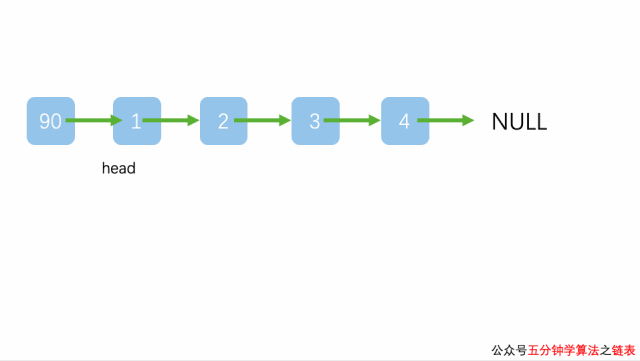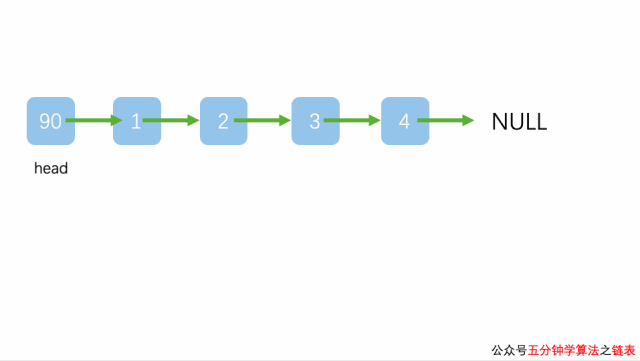
对于链表这种数据结构而言,在链表头或者链尾添加元素都非常方便。
将元素插入链表的中间位置也十分简单,不过得注意插入的顺序
Node insertNode = new Node(e); insertNode.next = prevNode.next; prevNode.next = insertNode;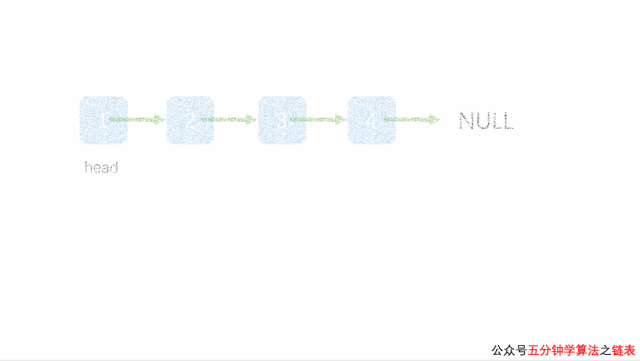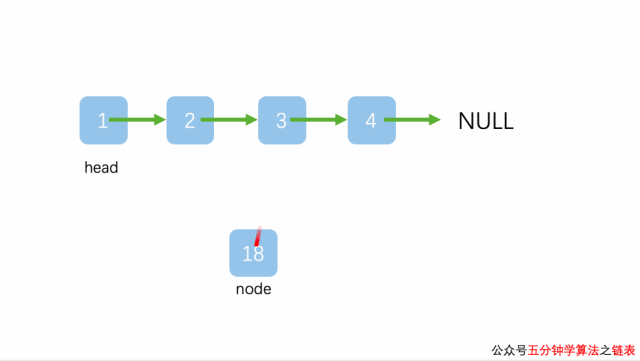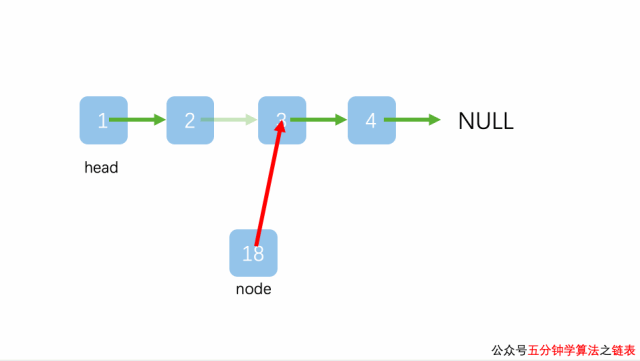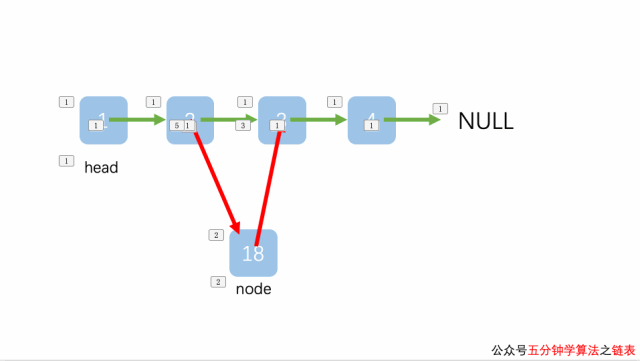
对比两组动画后,聪明的你很快就会想:能否用同样的代码来处理链表的插入头部和插入中间的操作呢?
答案是肯定的!只需要引入虚拟的头结点的概念就行了。
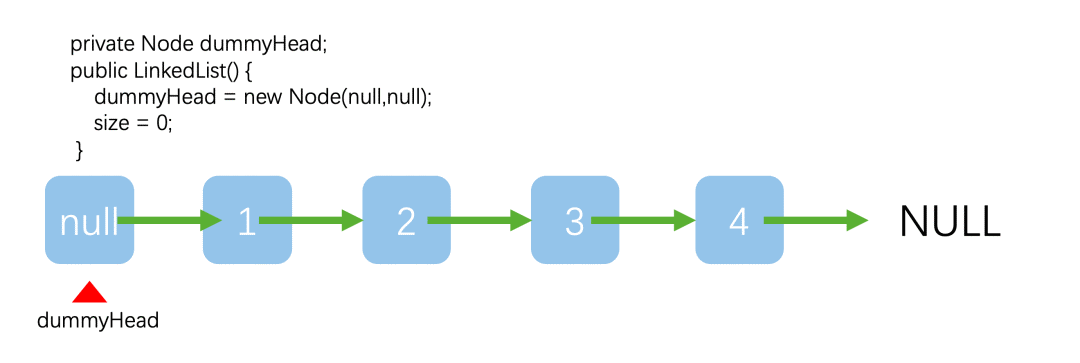
那么就可以得到链表的添加元素的代码:

链表的删除元素操作
对于链表的删除元素操作,需要找到目标节点的前驱节点。
prev.next = delNode.next delNode.next = null链表的查找元素操作
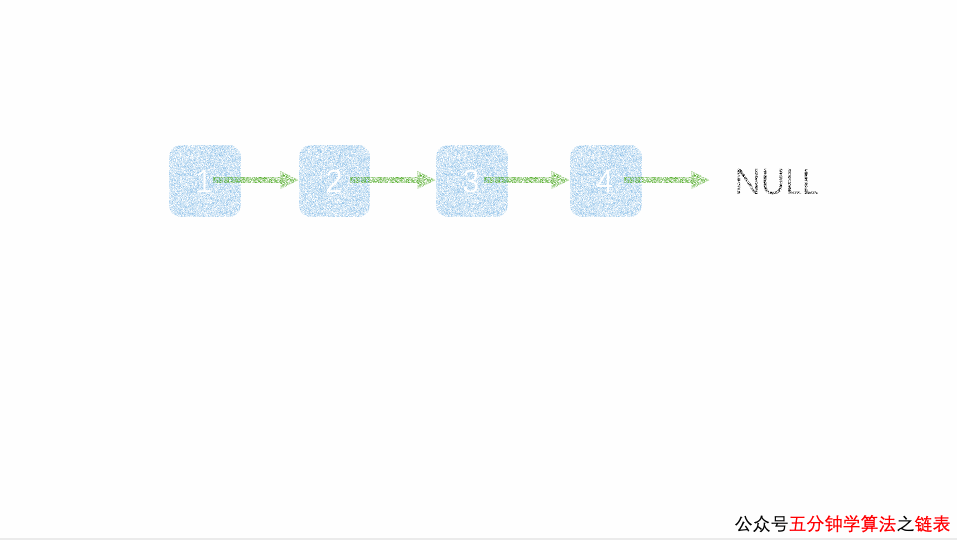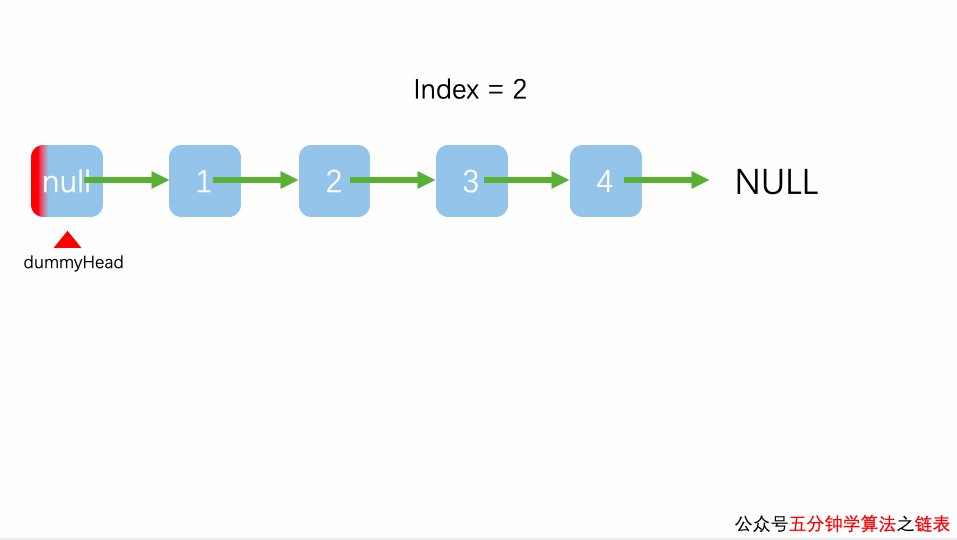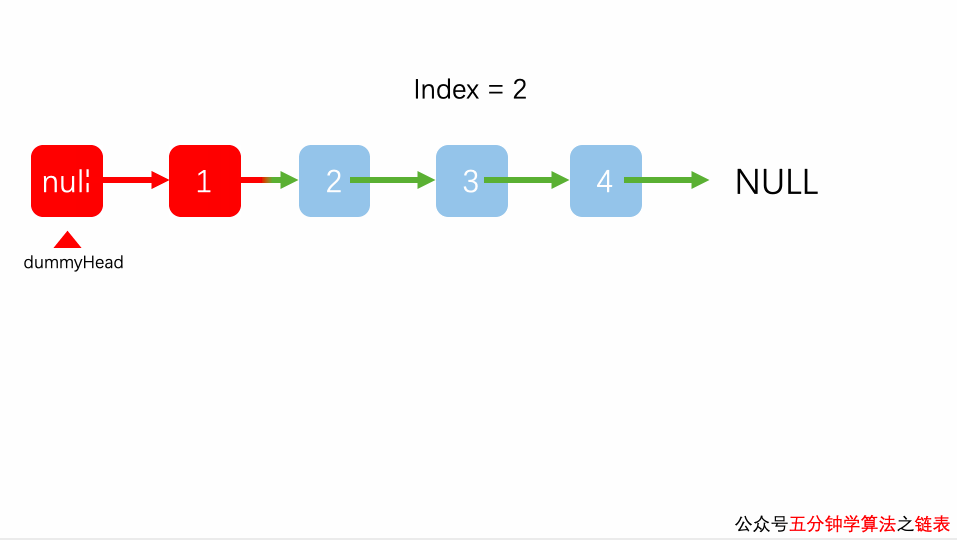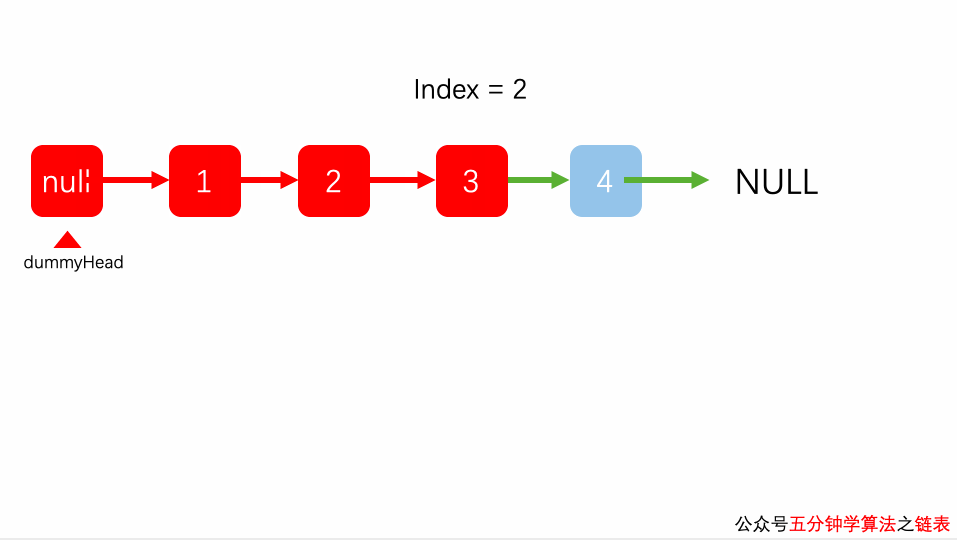
虚拟节点所在的位置索引可以视为 -1

链表的修改元素操作
基于上面 链表的查找元素操作 很容易写出 链表的修改元素操作

链表的时间复杂度
| 接口 | 说明 | 复杂度 |
|---|---|---|
| add(index, e) | 插入操作 | O(n) |
| remove(index, e) | 删除操作 | O(n) |
| set(index, e) | 修改操作 | O(n) |
| get(index, e) | 查找操作 | O(n) |
| contains(index, e) | 也是查找操作 | O(n) |
正因为链表没有索引,因此链表丧失了像数组那样快速访问的能力,这也就让链表的增删改查全都是O(n)级别的。
这看上去链表像是一个性能很差的数据结构,那链表是如何能在数据结构中穿针引线呢?
请继续阅读后续的内容:如何用链表实现栈和队列