1 前言
树是数据结构中的重中之重,尤其以各类二叉树为学习的难点。本文将详细讲述树的基本概念以及树构造和遍历,为后续深入学习做好基础。
2 概念
2.1 节点
节点:是数据结构中的基础,是构成复杂数据结构的基本组成单位。
2.2 树节点
本系列文章中提及的节点专指树的节点。例如:节点A表示为:

树节点A
3 树
3.1 定义
树(Tree)是n(n>=0)个节点的有限集。n=0时称为空树。在任意一颗非空树中:
(1)有且仅有一个特定的称为根(Root)的节点;
(2)当n>1时,其余节点可分为m(m>0)个互不相交的有限集T1、T2、……、Tn,其中每一个集合本身又是一棵树,并且称为根的子树。
此外,树的定义还需要强调以下两点:
(3)n>0时根节点是唯一的,不可能存在多个根节点,数据结构中的树只能有一个根节点。
(4)m>0时,子树的个数没有限制,但它们一定是互不相交的。
例如:图3.1中所示的树为一棵有10个节点的一般树。
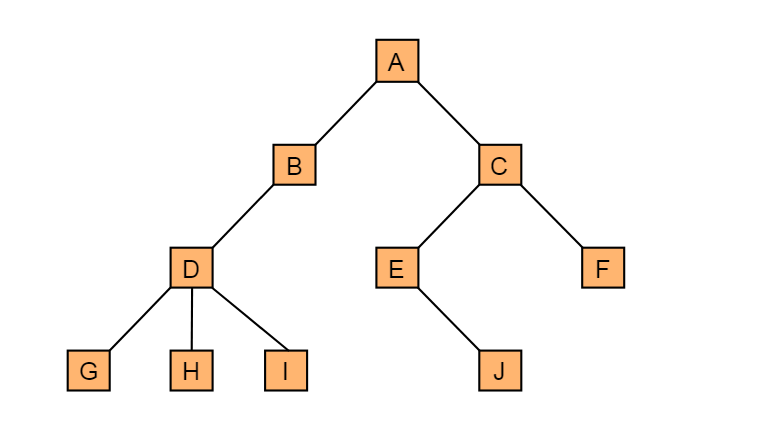
图3.1 一般树
由树的定义可以看出,树的定义使用了递归的方式。递归在树的学习过程中起着重要作用。
3.2 节点的度
定义:节点拥有的子树数目称为节点的度。例如:图3.2中标注了图3.1所示树的各个节点的度。
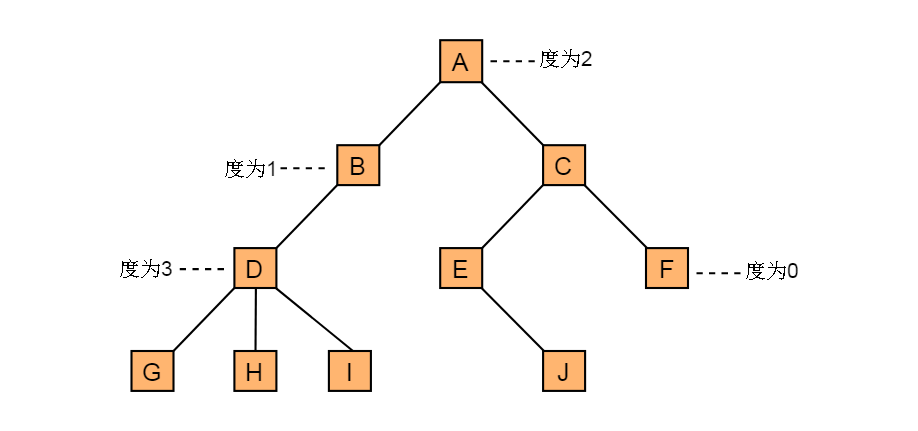
图3.2 节点的度
3.3 节点关系
节点子树的根节点为该节点的孩子节点。相应该节点称为孩子节点的双亲节点。图3.2中,A为B的双亲节点,B为A的孩子节点。
同一个双亲节点的孩子节点之间互称兄弟节点。图3.2中,B与C互为兄弟节点,GHI互为兄弟节点,EF互为兄弟节点。
3.4 节点层次
从根节点开始,根节点为第一层,根的孩子为第二层,以此类推。例如:图3.4表示了图3.1所示树的层次关系
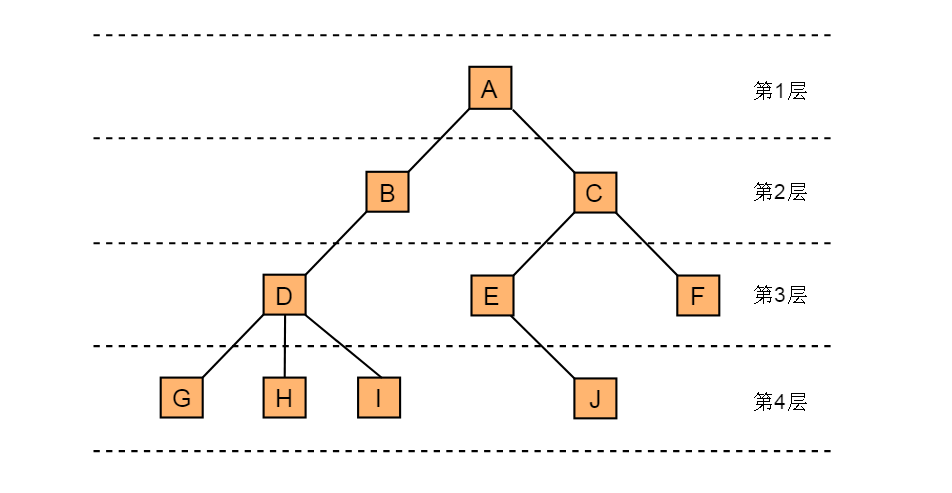
图3.4 节点层次
3.5 树的深度
树中节点的最大层次数称为树的深度或高度。例如:图3.1所示树的深度为4。
4 二叉树
4.1 定义
二叉树是n(n>=0)个节点的有限集合,该集合或者为空集(称为空二叉树),或者由一个根节点和两棵互不相交的、分别称为根节点的左子树和右子树组成。
图4.1展示了一棵一般二叉树:

图4.1 一般二叉树
4.2 二叉树特点
由二叉树的定义,以及图中所示的二叉树的分析可以得出二叉树具有以下几个特点:
(1)每个节点最多有两颗子树,所以二叉树中不存在度大于2的节点。
(2)左子树和右子树是有顺序的,次序不能任意颠倒。
(3)即使树中某节点只有一棵子树,也要区分它是左子树还是右子树。
4.3 二叉树性质
(1)在二叉树的第i层上最多有2i-1 个节点 。(i>=1)
(2)二叉树中如果深度为k,那么最多有2k-1个节点。(k>=1)
(3)n0=n2+1 n0表示度数为0的节点数,n2表示度数为2的节点数。
(4)在完全二叉树中,具有n个节点的完全二叉树的深度为[log2n]+1,其中[log2n]是向下取整。
(5)若对含 n 个节点的完全二叉树从上到下且从左至右进行 1 至 n 的编号,则对完全二叉树中任意一个编号为 i 的节点有如下特性:
(5)- 1,若 i=1,则该节点是二叉树的根,无双亲, 否则,编号为 [i/2] 的节点为其双亲节点;
(5)- 2,若 2i>n,则该节点无左孩子, 否则,编号为 2i 的节点为其左孩子节点;
(5)- 3,若 2i+1>n,则该节点无右孩子节点, 否则,编号为2i+1 的节点为其右孩子节点。
4.4 斜树
斜树:所有的节点都只有左子树的二叉树叫左斜树。所有节点都是只有右子树的二叉树叫右斜树,这两者统称为斜树。
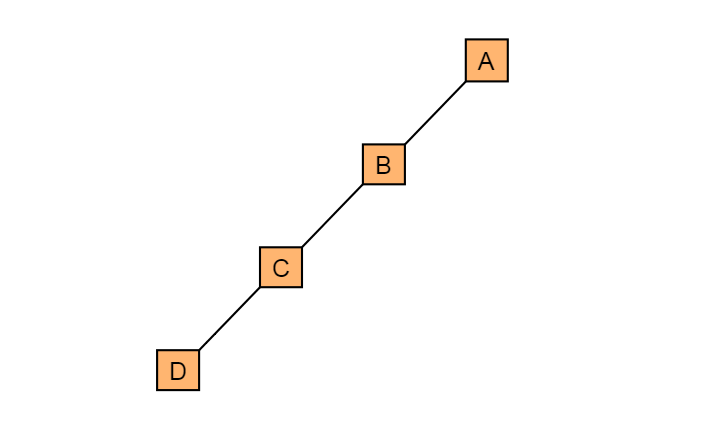
图4.4.1 左斜树
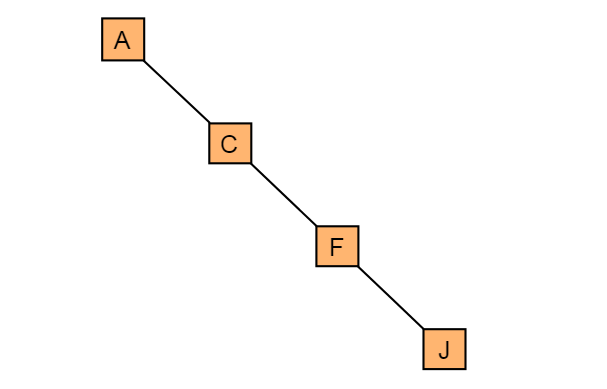
图4.4.2 右斜树
4.5 满二叉树
满二叉树:在一棵二叉树中。如果所有分支节点都存在左子树和右子树,并且所有叶子都在同一层上,这样的二叉树称为满二叉树。
满二叉树的特点有:
(1)叶子只能出现在最下一层。出现在其它层就不可能达成平衡。
(2)非叶子节点的度一定是2。
(3)在同样深度的二叉树中,满二叉树的节点个数最多,叶子节点数最多。

图4.5 满二叉树
4.6 完全二叉树
完全二叉树:对一颗具有n个节点的二叉树按层编号,如果编号为i(1<=i<=n)的节点与同样深度的满二叉树中编号为i的节点在二叉树中位置完全相同,则这棵二叉树称为完全二叉树。 图4.6为一棵完全二叉树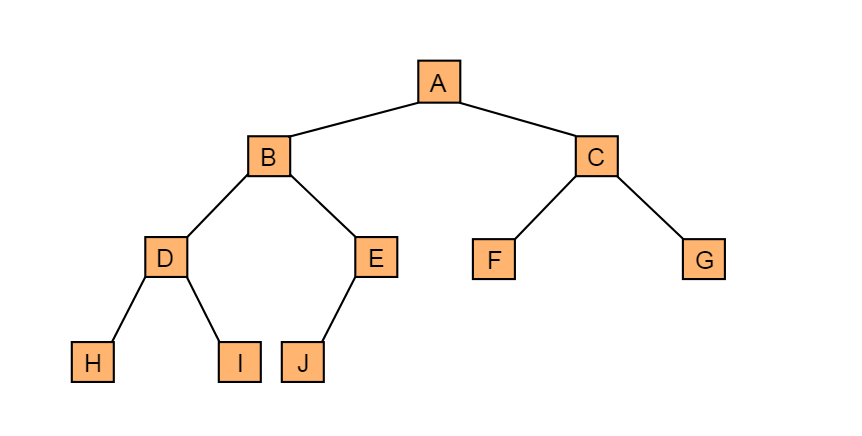
图4.6 完全二叉树
完全二叉树特点:
(1)叶子节点只能出现在最下层和次下层。
(2)最下层的叶子节点集中在树的左部。
(3)倒数第二层若存在叶子节点,一定在右部连续位置。
(4)如果节点度为1,则该节点只有左孩子,即没有右子树。
(5)同样节点数目的二叉树,完全二叉树深度最小。
注:满二叉树一定是完全二叉树,但反过来不一定成立。
4.7 二叉树的存储结构
(1)顺序存储
二叉树的顺序存储结构就是使用一维数组存储二叉树中的节点,并且节点的存储位置,就是数组的下标索引。
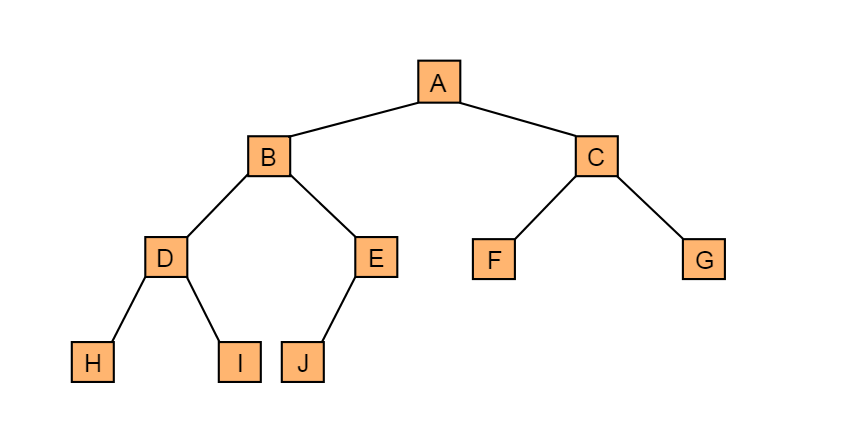
图4.6 完全二叉树
例如:图4.6所示的一棵完全二叉树采用顺序存储方式,如图4.7.1表示:
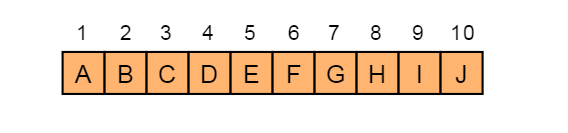
图4.7.1 顺序存储
由图4.7.1可以看出,当二叉树为完全二叉树时,节点数刚好填满数组。那么当二叉树不为完全二叉树时,采用顺序存储形式如何呢?例如:对于图4.7.2描述的二叉树:
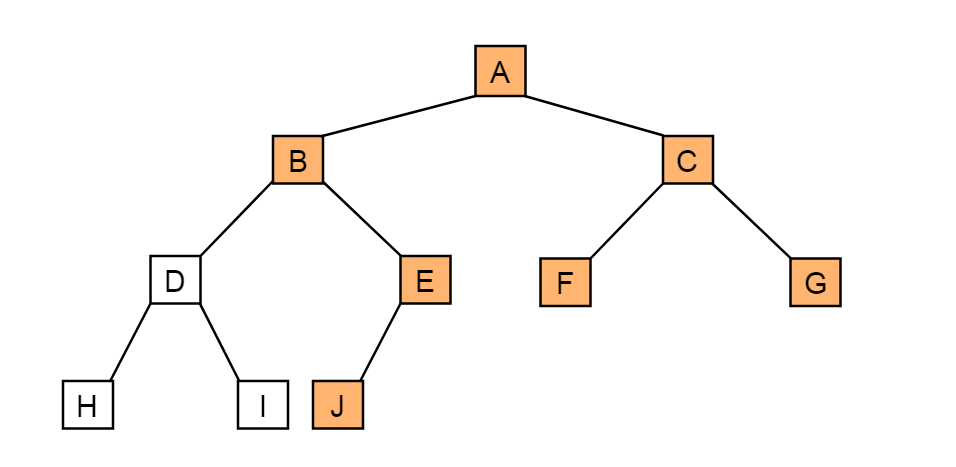
图4.7.2
其中,未填充节点表示节点不存在。那么图4.7.2所示的二叉树的顺序存储结构如图4.7.3所示:

图4.7.3
其中,∧表示数组中此位置没有存储节点。此时可以发现,顺序存储结构中已经出现了空间浪费的情况。
那么对于图4.4.2所示的右斜树极端情况对应的顺序存储结构如图4.7.4所示:
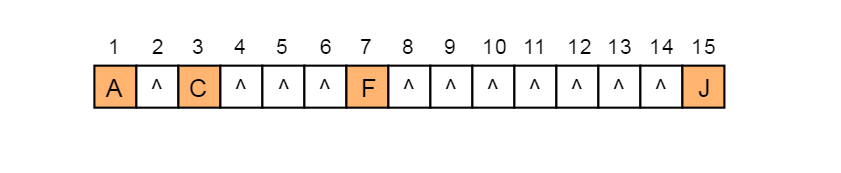
图4.7.4
由图4.7.4可以看出,对于这种右斜树极端情况,采用顺序存储的方式是十分浪费空间的。因此,顺序存储一般适用于完全二叉树。
(2)二叉链表
既然顺序存储不能满足二叉树的存储需求,那么考虑采用链式存储。由二叉树定义可知,二叉树的每个节点最多有两个孩子。因此,可以将节点数据结构定义为一个数据和两个指针域。表示方式如图4.7.5所示:
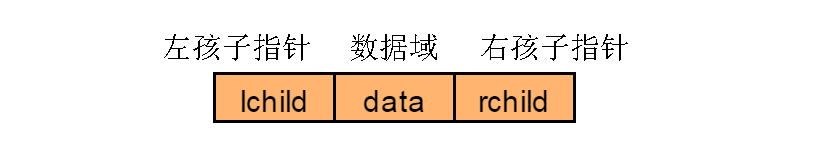
图4.7.5
定义节点代码:
typedef struct BiTNode{
TElemType data;//数据
struct BiTNode *lchild, *rchild;//左右孩子指针
} BiTNode, *BiTree; 则图4.6所示的完全二叉树可以采用图4.7.6表示。
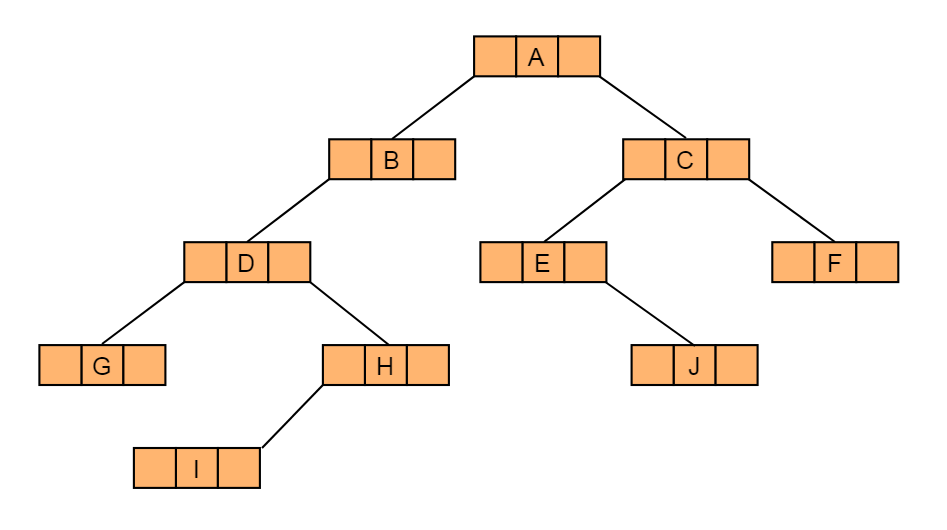
图4.7.6
图4.7.6中采用链表结构存储二叉树,这种链表称为二叉链表。
5 二叉树遍历
5.1 定义
二叉树的遍历是指从二叉树的根节点出发,按照某种次序依次访问二叉树中的所有节点,使得每个节点被访问一次,且仅被访问一次。按照二叉树的访问次序,可以将二叉树遍历分为四种:
(1)前序遍历
(2)中序遍历
(3)后序遍历
(4)层序遍历
5.2 前序遍历
前序遍历,通俗的说就是从二叉树的根节点出发,当第一次到达节点时就输出节点数据,按照先向左在向右的方向访问。
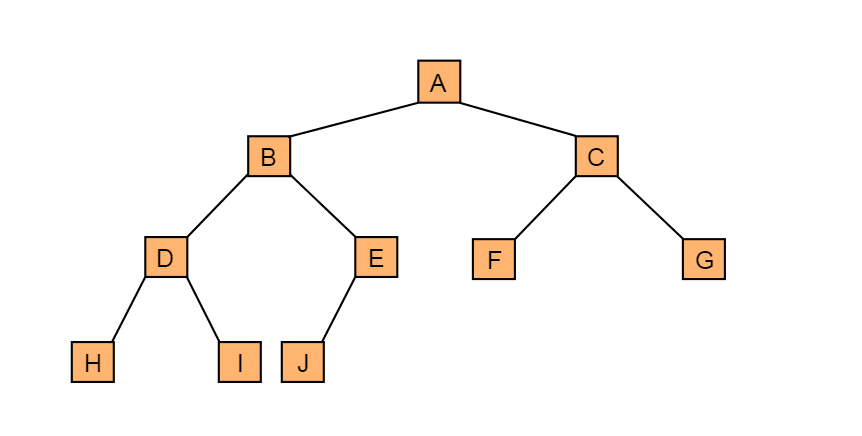
图5.2
例如:图5.2所示二叉树采用前序遍历方式访问如下:
(1)从根节点出发,则第一次到达节点A,故输出A;
(2)继续向左访问,第一次访问节点B,故输出B;
(3)按照同样规则,输出D,输出H;
(4)当到达叶子节点H,返回到D,此时已经是第二次到达D,故不在输出D
(5)向D右子树访问,D右子树不为空,则访问至I,第一次到达I,则输出I;
(6)I为叶子节点,则返回到D,D左右子树已经访问完毕,则返回到B,
(7)访问B右子树,第一次到达E,故输出E;
(8)访问E左子树,故输出J;
(9)按照同样的访问规则,继续输出C、F、G;
则图5.2所示二叉树的前序遍历输出为:
A-B-D-H-I-E-J-C-F-G
5.3 中序遍历
中序遍历就是从二叉树的根节点出发,当第二次到达节点时就输出节点数据,按照先向左在向右的方向访问。
例如:图5.2所示二叉树中序访问如下:
(1)从根节点出发,则第一次到达节点A,不输出A;
(2)继续向左访问,第一次访问节点B,不输出B;
(3)继续到达D,H,到达H,H左子树为空,则返回到H,此时第二次访问H,故输出H;
(4)H右子树为空,则返回至D,此时第二次到达D,故输出D;
(5)由D返回至B,第二次到达B,故输出B;
(6)按照同样规则继续访问,输出J、E、A、F、C、G;
则5.2所示二叉树的中序遍历输出为:
H-D-I-B-J-E-A-F-C-G
5.4 后序遍历
后序遍历就是从二叉树的根节点出发,当第三次到达节点时就输出节点数据,按照先向左在向右的方向访问。
例如:图5.2所示二叉树后序访问如下:
(1)从根节点出发,则第一次到达节点A,不输出A;
(2)继续向左访问,第一次访问节点B,不输出B;
(3)继续到达D,H,到达H,H左子树为空,则返回到H,此时第二次访问H,不输出H;
(4)H右子树为空,则返回至H,此时第三次到达H,故输出H;
(5)由H返回至D,第二次到达D,不输出D;
(6)继续访问至I,I左右子树均为空,故第三次访问I时,输出I;
(7)返回至D,此时第三次到达D,故输出D;
(8)按照同样规则继续访问,输出J、E、B、F、G、C,A;
则图5.2所示二叉树的后序遍历输出为:
H-I-D-J-E-B-F-G-C-A
虽然二叉树的遍历过程看似繁琐,但是由于二叉树是一种递归定义的结构,故采用递归方式遍历二叉树的代码十分简单。
5.5 遍历程序
递归实现代码如下:
/*二叉树的前序遍历递归算法*/
void PreOrderTraverse(BiTree T)
{
if(T==NULL)
return;
printf("%c", T->data); /*显示节点数据,可以更改为其他对节点操作*/
PreOrderTraverse(T->lchild); /*再先序遍历左子树*/
PreOrderTraverse(T->rchild); /*最后先序遍历右子树*/
}
/*二叉树的中序遍历递归算法*/
void InOrderTraverse(BiTree T)
{
if(T==NULL)
return;
InOrderTraverse(T->lchild); /*中序遍历左子树*/
printf("%c", T->data); /*显示节点数据,可以更改为其他对节点操作*/
InOrderTraverse(T->rchild); /*最后中序遍历右子树*/
}
/*二叉树的后序遍历递归算法*/
void PostOrderTraverse(BiTree T)
{
if(T==NULL)
return;
PostOrderTraverse(T->lchild); /*先后序遍历左子树*/
PostOrderTraverse(T->rchild); /*再后续遍历右子树*/
printf("%c", T->data); /*显示节点数据,可以更改为其他对节点操作*/
}5.6 层次遍历
层次遍历就是按照树的层次自上而下的遍历二叉树。针对图5.2所示二叉树的层次遍历结果为:
A-B-C-D-E-F-G-H-I-J
5.7 考点
(1)已知前序遍历序列和中序遍历序列,确定一棵二叉树。
例题:若一棵二叉树的前序遍历为ABCDEF,中序遍历为CBAEDF,请画出这棵二叉树。
分析:前序遍历第一个输出节点为根节点,故A为根节点。早中序遍历中根节点处于左右子树节点中间,故节点A的左子树中节点有CB,右子树中节点有EDF。
如图5.7.1所示:
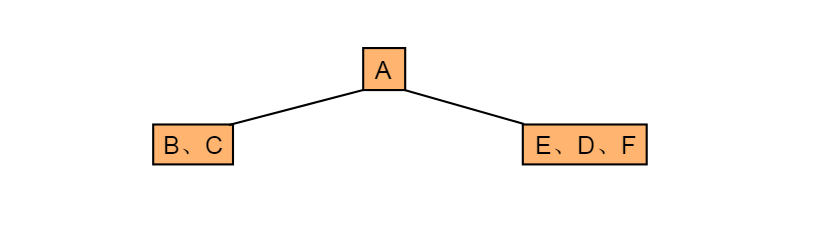
图5.7.1
按照同样的分析方法,对A的左右子树进行划分,最后得出二叉树的形态如图5.7.2所示:
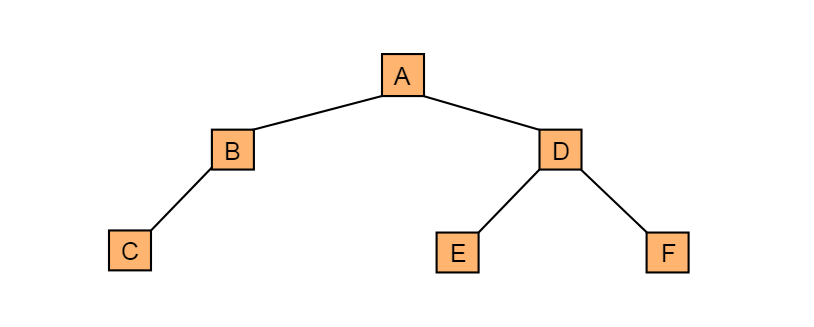
图5.7.2
(2)已知后序遍历序列和中序遍历序列,确定一棵二叉树。
后序遍历中最后访问的为根节点,因此可以按照上述同样的方法,找到根节点后分成两棵子树,进而继续找到子树的根节点,一步步确定二叉树的形态。
注:已知前序遍历序列和后序遍历序列,不可以唯一确定一棵二叉树。
6 结语
通过上述的介绍,已经对于二叉树有了初步的认识。本篇文章介绍的基础知识希望读者能够牢牢掌握,并且能够在脑海中建立一棵二叉树的模型,为后续学习打好基础。





