1 概念
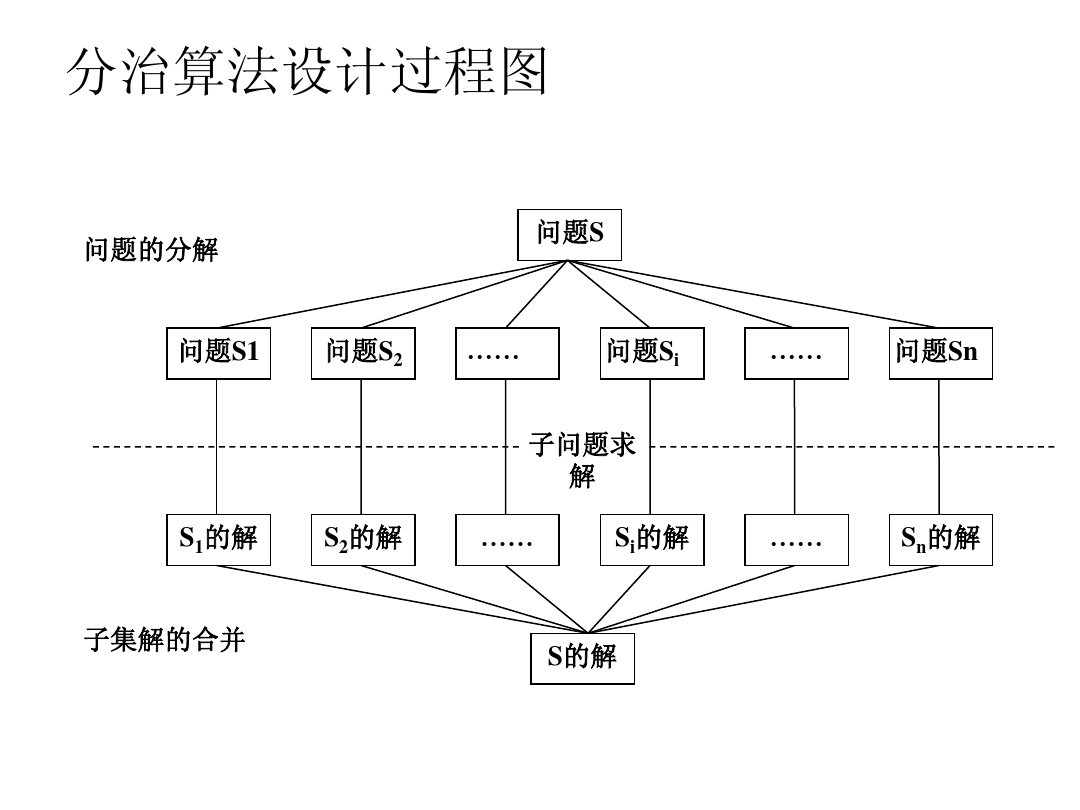
分治算法,根据字面意思解释是“分而治之”,就是把一个复杂的问题分成两个或更多的相同或相似的子问题,再把子问题分成更小的子问题……直到最后子问题可以简单的直接求解,原问题的解即子问题的解的合并。
2 算法策略
分治策略:对于一个规模为n的问题,若该问题可以容易地解决(比如说规模n较小)则直接解决,否则将其分解为k个规模较小的子问题,这些子问题互相独立且与原问题形式相同,递归地解这些子问题,然后将各子问题的解合并得到原问题的解。
在平时日常生活中,分治思想也是随处可见的。例如:当我们打牌时,在进行洗牌时,若牌的数目较多,一个人洗不过来,则会将牌进行分堆,单独洗一小堆牌是相对容易的,每一堆牌都洗完之后再放到一起,则完成洗牌过程。
3 使用场景
(1)该问题的规模缩小到一定的程度就可以容易地解决。
(2)该问题可以分解为若干个规模较小的相同问题,即该问题具有最优子结构性质。
(3)利用该问题分解出的子问题的解可以合并为该问题的解。
(4)该问题所分解出的各个子问题是相互独立的,即子问题之间不包含公共的子问题。
4 基本步骤
分治法在每一层递归上都有三个步骤:
(1)分解:将原问题分解为若干个规模较小,相互独立,与原问题形式相同的子问题。
(2)求解:若子问题规模较小而容易被解决则直接解,否则递归地解各个子问题。
(3)合并:将各个子问题的解合并为原问题的解。
5 伪代码
Divide-and-Conquer(P)
if |P| ≤ n0
then return(ADHOC(P))
将P分解为较小的子问题 P1 ,P2 ,...,Pk
for i←1 to k
do yi ← Divide-and-Conquer(Pi) △ 递归解决Pi
T ← MERGE(y1,y2,...,yk) △ 合并子问题
return(T)其中,|P|表示问题P的规模,n0为一阈值,表示当问题P的规模不超过n0时,问题已容易直接解出,不必再继续分解。ADHOC(P)是该分治法中的基本子算法,用于直接解小规模的问题P。因此,当P的规模不超过n0时直接用算法ADHOC(P)求解。算法MERGE(y1,y2,…,yk)是该分治法中的合并子算法,用于将P的子问题P1 ,P2 ,…,Pk的相应的解y1,y2,…,yk合并为P的解。
6 典型案例
6.1 二分查找
二分查找是典型的分治算法的应用。需要注意的是,二分查找的前提是查找的数列是有序的。
算法流程:
(1)选择一个标志i将集合分为二个子集合。
(2)判断标志L(i)是否能与要查找的值des相等,相等则直接返回。
(3)否则判断L(i)与des的大小。
(4)基于判断的结果决定下步是向左查找还是向右查找。
(5)递归继续上面的步骤。
通过二分查找的流程可以看出,二分查找是将原有序数列划分为左右两个子序列,然后在对两个子序列中的其中一个在进行划分,直至查找成功。
代码实现:
#include
#include
int k;
int binarysearch(int a[],int x,int low,int high)//a表示需要二分的有序数组(升序),x表示需要查找的数字,low,high表示高低位
{
if(low>high)
{
return -1;//没有找到
}
int mid=(low+high)/2;
if(x==a[mid])//找到x
{
k=mid;
return x;
}
else if(x>a[mid]) //x在后半部分
{
binarysearch(a,x,mid+1,high);//在后半部分继续二分查找
}
else//x在前半部分
{
binarysearch(a,x,low,mid-1);
}
}
int main()
{
int a[10]={1,2,3,4,5,6,7,8,9,10};
printf("请输入需要查找的正数字:\n");
int x;
scanf("%d",&x);
int r=binarysearch(a,x,0,9);
if(r==-1)
{
printf("没有查到\n");
}
else
{
printf("查到了,在数列的第%d个位置上\n",k+1);
}
return 0;
} 6.2 全排列问题
问题描述:
有1,2,3,4个数,问你有多少种排列方法,并输出排列。
问题分析:
若采用分治思想进行求解,首先需要把大问题分解成很多的子问题,大问题是所有的排列方法。那么我们分解得到的小问题就是以1开头的排列,以2开头的排列,以3开头的排列,以4开头的排列。现在这些问题有能继续分解,比如以1开头的排列中,只确定了1的位置,没有确定2,3,4的位置,把2,3,4三个又看成大问题继续分解,2做第二个,3做第二个,或者4做第二个。一直分解下去,直到分解成的子问题只有一个数字的时候,不能再分解。只有一个数的序列只有一种排列方式,则子问题求解容易的多。
代码实现:
public class Test {
public static void main(String[] args) {
int[] arr = { 1, 2, 3, 4 };
fullSort(arr, 0, arr.length - 1);
}
public static void fullSort(int[] arr, int start, int end) {
// 递归终止条件
if (start == end) {
for (int i : arr) {
System.out.print(i);
}
System.out.println();
return;
}
for (int i = start; i <= end; i++) {
swap(arr, i, start);
fullSort(arr, start + 1, end);
swap(arr, i, start);
}
}
private static void swap(int[] arr, int i, int j) {
int tmp = arr[i];
arr[i] = arr[j];
arr[j] = tmp;
}
}6.3 归并排序
归并排序:归并(Merge)排序法是将两个(或两个以上)有序表合并成一个新的有序表,即把待排序序列分为若干个子序列,每个子序列是有序的。然后再把有序子序列合并为整体有序序列。 即先划分为两个部分,最后进行合并。

归并排序
伪代码:
算法 MergeSort(A, p, r)
输入:数组A[p...r]
输出:有序数组A
if(p < r)
then q <- (p+r)/2//折半划分
MergeSort(A, p ,q)//子问题1
MergeSort(A, p ,q)//子问题2
Merge(A, p ,q, r)//合并求解代码实现:
public class MergeSort {
//两路归并算法,两个排好序的子序列合并为一个子序列
public void merge(int []a,int left,int mid,int right){
int []tmp=new int[a.length];//辅助数组
int p1=left,p2=mid+1,k=left;//p1、p2是检测指针,k是存放指针
while(p1<=mid && p2<=right){
if(a[p1]<=a[p2])
tmp[k++]=a[p1++];
else
tmp[k++]=a[p2++];
}
while(p1<=mid) tmp[k++]=a[p1++];//如果第一个序列未检测完,直接将后面所有元素加到合并的序列中
while(p2<=right) tmp[k++]=a[p2++];//同上
//复制回原素组
for (int i = left; i <=right; i++)
a[i]=tmp[i];
}
public void mergeSort(int [] a,int start,int end){
if(start6.4 快速排序
快速排序的基本思想:当前待排序的无序区为A[low..high],利用分治法可将快速排序的基本思想描述为:
(1)分解:
在A[low..high]中任选一个记录作为基准(pivot),以此基准将当前无序区划分为左、右两个较小的子区间R[low..pivotpos-1)和R[pivotpos+1..high],并使左边子区间中所有记录的关键字均小于等于基准记录(不妨记为pivot)的关键字pivot.key,右边的子区间中所有记录的关键字均大于等于pivot.key,而基准记录pivot则位于正确的位置(pivotpos)上,它无须参加后续的排序。
(2)求解:
通过递归调用快速排序对左、右子区间R[low..pivotpos-1]和R[pivotpos+1..high]快速排序。
(3)合并:
因为当"求解"步骤中的两个递归调用结束时,其左、右两个子区间已有序。对快速排序而言,"组合"步骤无须做什么,可看作是空操作。

快速排序
代码实现:
#include
using namespace std;
void QuickSort(int arr[], int low, int high){
if (high <= low) return;
int i = low;
int j = high + 1;
int key = arr[low];
while (true)
{
/*从左向右找比key大的值*/
while (arr[++i] < key)
{
if (i == high){
break;
}
}
/*从右向左找比key小的值*/
while (arr[--j] > key)
{
if (j == low){
break;
}
}
if (i >= j) break;
/*交换i,j对应的值*/
int temp = arr[i];
arr[i] = arr[j];
arr[j] = temp;
}
/*中枢值与j对应值交换*/
int temp = arr[low];
arr[low] = arr[j];
arr[j] = temp;
QuickSort(arr, low, j - 1);
QuickSort(arr, j + 1, high);
} 6.5 汉诺塔
问题描述:
有三根杆子A,B,C。A杆上有若干碟子,且碟子是按照由小到大向下叠放。每次移动一块碟子,且小的只能叠在大的上面,把所有碟子从A杆全部移到C杆上。
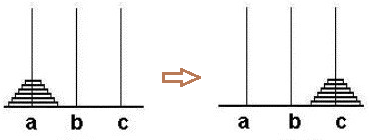
问题分析:
对圆盘编号1~n,数字大的圆盘比数字小的圆盘体积大。并且引入起始塔,中转塔,目标塔的概念,在算法运行的时候,这3个塔的身份可能会互相变换。则汉诺塔问题的求解思想如下:
(1)如果现在在塔A上面只有1个圆盘,那么直接把圆盘移动到塔C即可;
(2)如果现在在塔A上面有2个圆盘,那么先把圆盘1从塔A移动到塔B,再把圆盘2从塔A移动到塔C,最后把圆盘1从塔B移动到塔C;
(3).……
(4)如果塔A有n个圆盘,那么需要先把圆盘n之前的(圆盘n-1~ 圆盘1)从塔A先移动到塔B,再把圆盘n从塔A移动到塔C,最后把放在塔B的(圆盘n-1~圆盘1)从塔B移动到塔C。
可以看出,汉诺塔问题的求解同样运用了分治算法的思想。
代码实现:
public static void hanoi(int n, String sourceTower, String tempTower, String targetTower) {
if (n == 1) {
//如果只有一个盘子1,那么直接将其从sourceTower移动到targetTower
move(n, sourceTower, targetTower);
} else {
//将(盘子n-1~盘子1)由sourceTower经过targetTower移动到tempTower
hanoi(n - 1, sourceTower, targetTower, tempTower);
//移动盘子n由sourceTower移动到targetTower
move(n, sourceTower, targetTower);
//把之前移动到tempTower的(盘子n-1~盘子1),由tempTower经过sourceTower移动到targetTower
hanoi(n - 1, tempTower, sourceTower, targetTower);
}
}
//盘子n的从sourceTower->targetTower的移动
private static void move(int n, String sourceTower, String targetTower) {
System.out.println("第" + n + "号盘子 move:" + sourceTower + "--->" + targetTower);
}7 总结分析
分治法将规模为n的问题分成k个规模为n/m的子问题去解。设分解阀值n0=1,且adhoc解规模为1的问题耗费1个单位时间。再设将原问题分解为k个子问题以及用merge将k个子问题的解合并为原问题的解需用f(n)个单位时间。用T(n)表示该分治法解规模为|P|=n的问题所需的计算时间,则有:
T(n)= k T(n/m)+f(n)





