大家好,我是吴师兄。
如果有人问你,计算机算法世界中最伟大的大师是有哪些?
你的答案是什么?
我的答案里面必然会有 Don E.Knuth。
KMP 算法、洗牌算法这些耳熟能详的的牛逼算法就是老爷子的创造,他的经典著作《计算机程序设计艺术》更是被誉为算法中“真正”的圣经。
一般说来,不知道此人的程序员是不可原谅的。
但据说,这位至高神面对 LeetCode 上的一道简单题,却花费了 24 小时才解出来,并且我只见过一个人(注:Keith Amling)用更短时间解出此题。
来源:LeetCode 287 评论区。

这道题目有什么神奇之处呢?
我们今天就来一探究竟!
依旧先给没有见过这道题目的小伙伴补充一下前置知识,LeetCode 第 287 号问题 寻找重复数 讲的是,给定一个包含 n + 1 个整数的数组 nums ,其数字都在 [1, n] 范围内(包括 1 和 n),可知至少存在一个重复的整数。
假设 nums 只有一个重复的整数,这个数可能出现两次或者多次,返回这个重复的数。
题目要求我们必须不修改数组 nums ,并且只用常量级 O(1) 的额外空间。
一眼扫过去,题目很好理解,思路也很容易理清,最直观的想法就是使用哈希表不就能马上查找出重复的整数么?
但再看一眼条件,只能用常量级 O(1) 的额外空间,于是哈希表的思路走不通。
一般的解法是采取二分查找的思路来解决,这里简单给大家介绍一下操作:
1、原始数组 nums 中总共包含了 n + 1 个整数,并且这些整数都在 [1, n] 范围内,那么如果设置 n 个抽屉,1 号抽屉存放 1 号整数、2 号抽屉存放 2 号整数、以此类推,那么总是有一个抽屉会至少存放两个数,这个数就是重复的数。
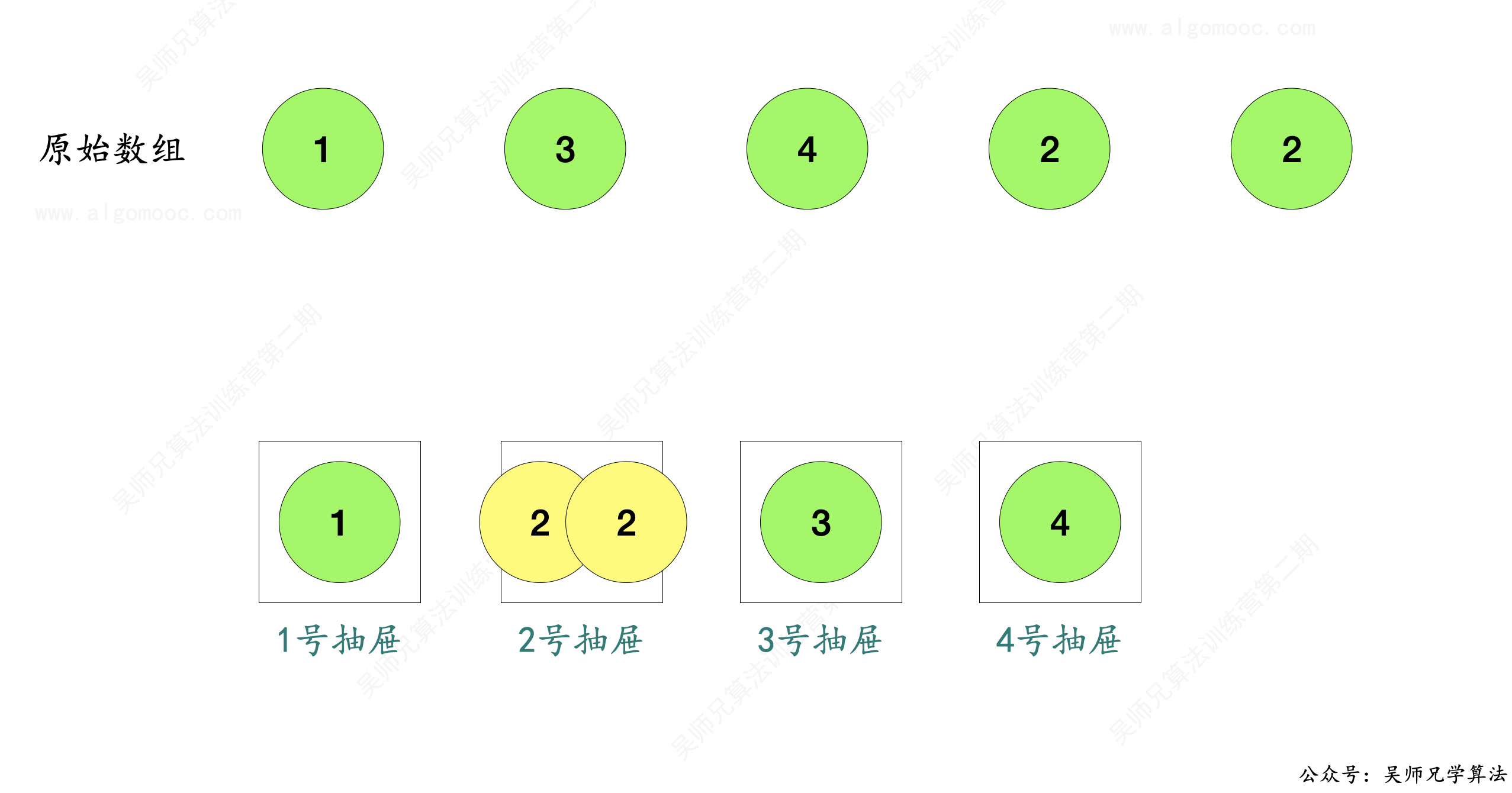
这个结论来自于抽屉原理:如果每个抽屉代表一个集合,每一个苹果就可以代表一个元素,假如有 n + 1 个元素放到 n 个集合中去,其中必定有一个集合里至少有两个元素。
2、接下来,设置两个指针, left 指向最小值 1,right 指向最大值 nums.length - 1,以上图为例,此时 left = 1 ,right = 4 。
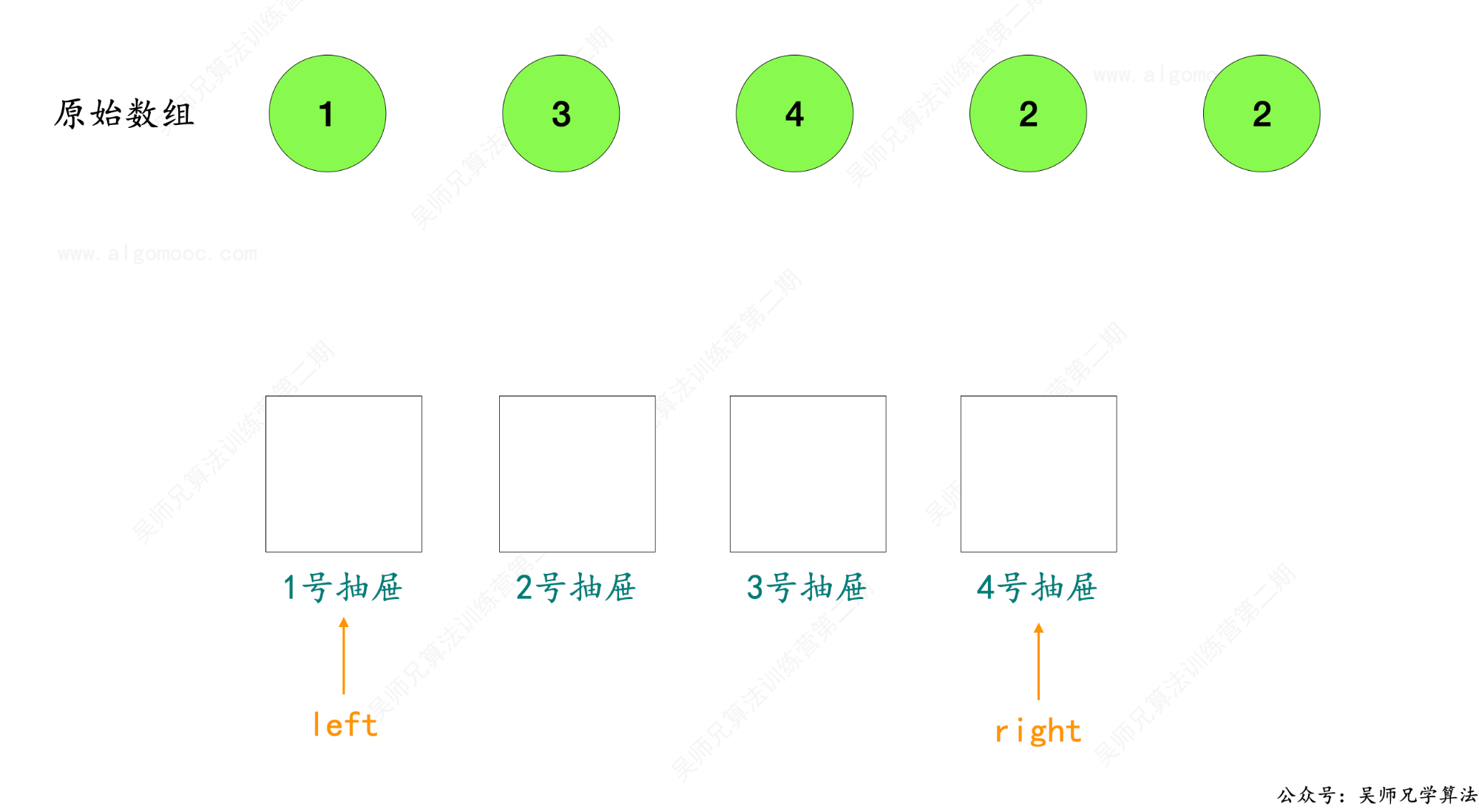
3、取 left 和 right 的中间值 mid = ( left + right ) / 2 ,所有的抽屉被划分为两块区间,[ left , mid ] 和 [ mid + 1 , right ],如果我们知道重复数字会出现在其中一块区间,那么另外一块区间根本不需要去管,不用再去存放数字。
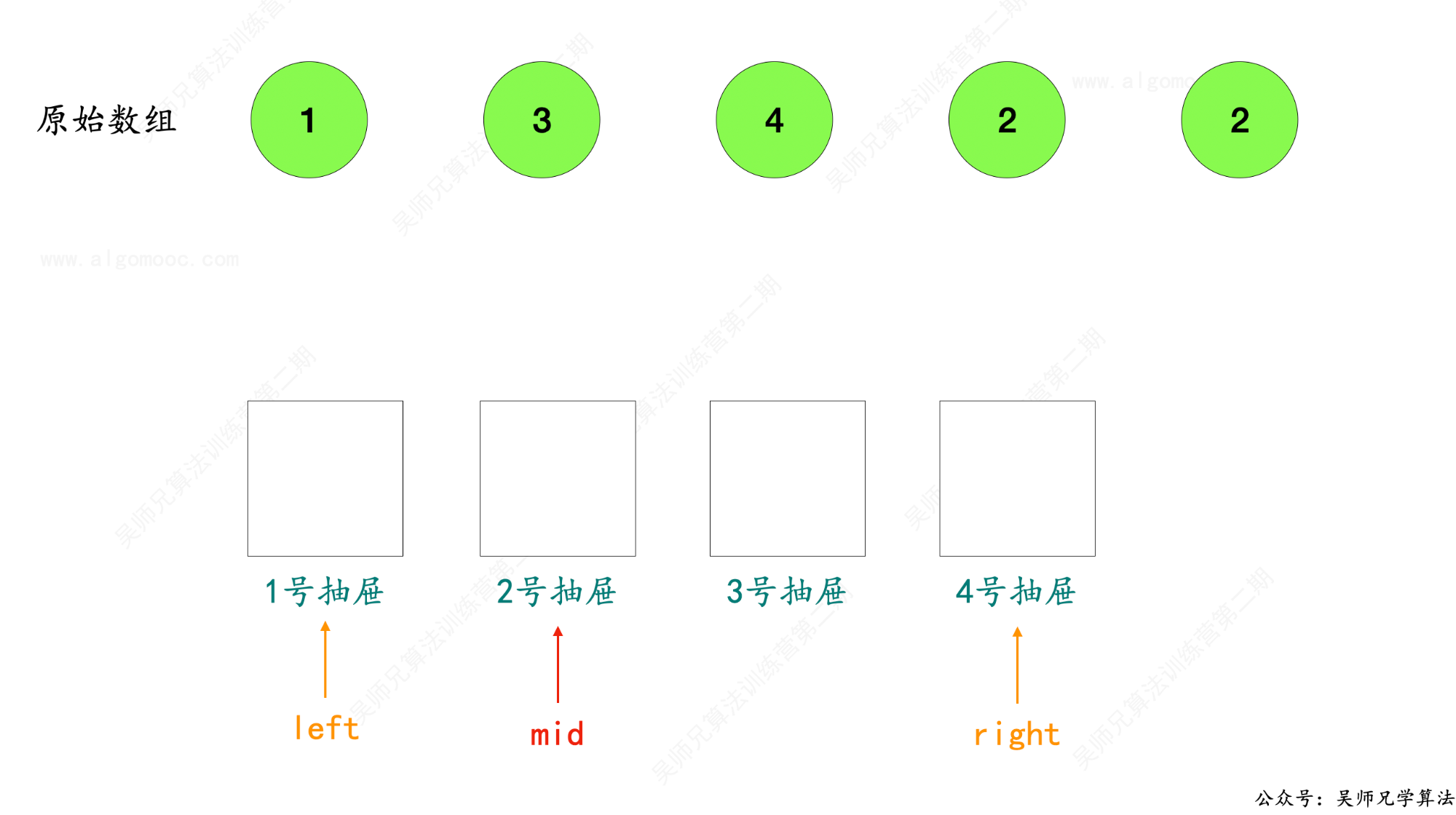
4、统计原始数组 nums 中小于等于 mid 元素的个数 count,此时发现 count = 3,而 [ left , mid ] 只包含了两个抽屉,那么根据抽屉原理,必然会出现两个数挤在相同的抽屉里面。


5、因此,3 号抽屉、4 号抽屉无需再去考虑,只需要考虑 1 号抽屉、2 号抽屉,到底是哪个抽屉存放了重复的数。
6、此时,抽屉的范围发生了变化,由原来的 [ 1 , 4 ] 变成了 [ 1 , 2 ],即 left 不变,right 变成了 2。
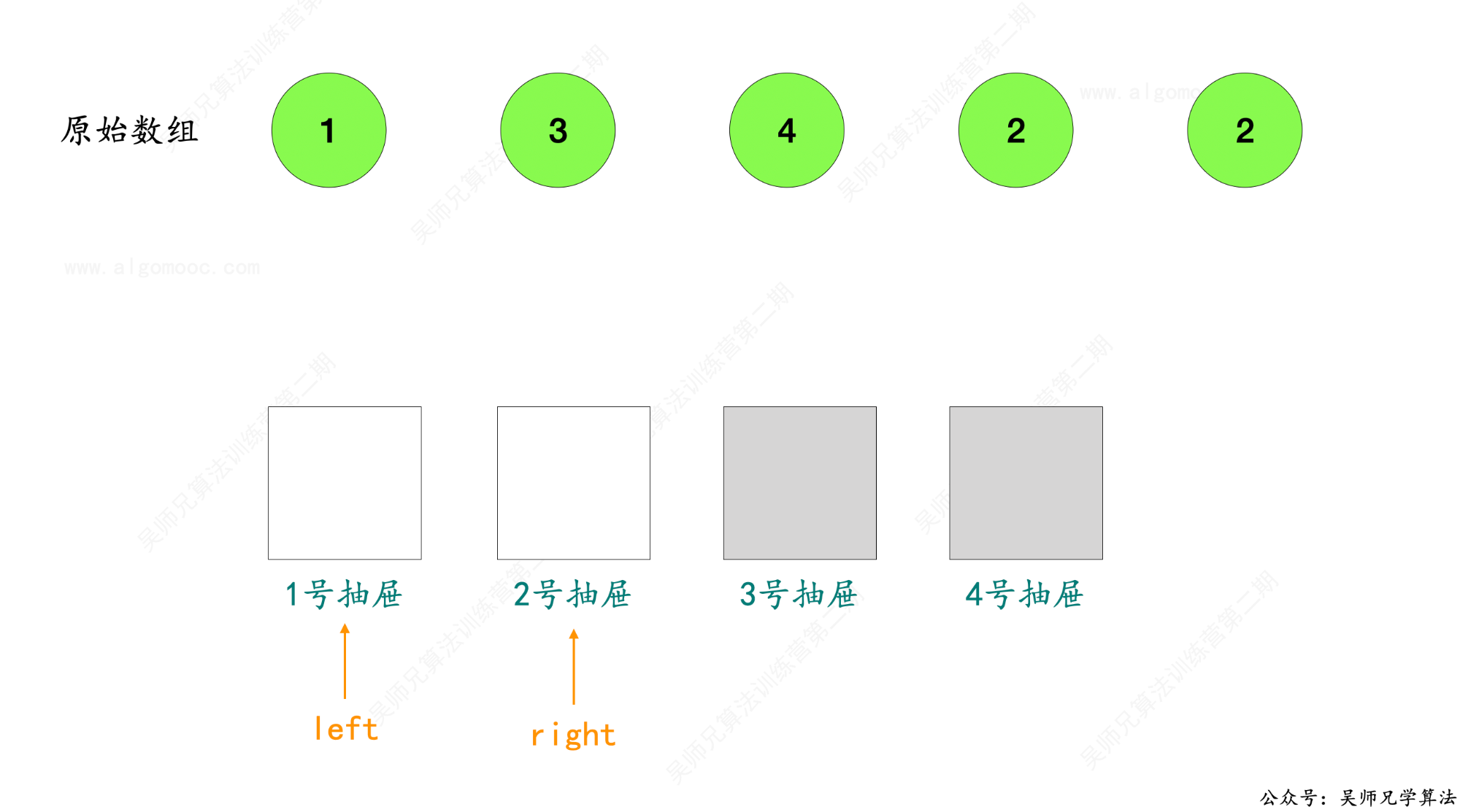
7、接下来,继续将 left 和 right 的区间划分为两块区间,[ 1 , 1 ] 和 [ 2 , 2 ],此时,mid = 1 ,统计原始数组 nums 中小于等于 mid 元素的个数 count,发现 count = 1,说明 [ 1 , 1 ]这个区间只有一个抽屉一个整数,那么肯定不存在重复的数,重复的数在 [ 2 , 2 ] 这个区间。
8、此时,抽屉的范围发生了变化,由原来的 [ 1 , 2 ] 变成了 [ 2 , 2 ],即 right 不变,left 变成了 2。
9、当前区间只有一个抽屉,也就说明是这个抽屉存放了重复的数,抽屉的编号是 2,说明重复的数字就是 2,找到答案了。
代码如下:
class Solution {
public int findDuplicate(int[] nums) {
int left = 1 ;
int right = nums.length - 1 ;
while ( left < right ) {
int mid = ( left + right ) / 2 ;
int count = 0;
for ( int num : nums) {
if ( num <= mid ){
count++ ;
}
}
if ( count > mid) {
right = mid ;
}else{
left = mid + 1;
}
}
return left;
}
}由此,这道题目也就解决了,Don E.Knuth 不至于 24 小时还想不出来吧?
问题出在优化!
二分查找解决的代码时间复杂度是O(nlogn),在面试的时候,面试官会问:还能不能再优化一下呢?
比如,LeetCode 的留言区就有同学懊恼的记录:今天美团面试考了这道题。作出一个解法以为完事了,结果连着追问好几种,整出翔了。

如果执着于二分查找的思路去优化,答案是无果,优化的方向是使用快慢指针。
具体操作如下:
1、对于原始数组 nums 来说,每个数字都有其对应的唯一索引 index,对于每个 index ,可以将其所对应的数字作为它下一个指向的对象,将这些对象串联为链表的形式。
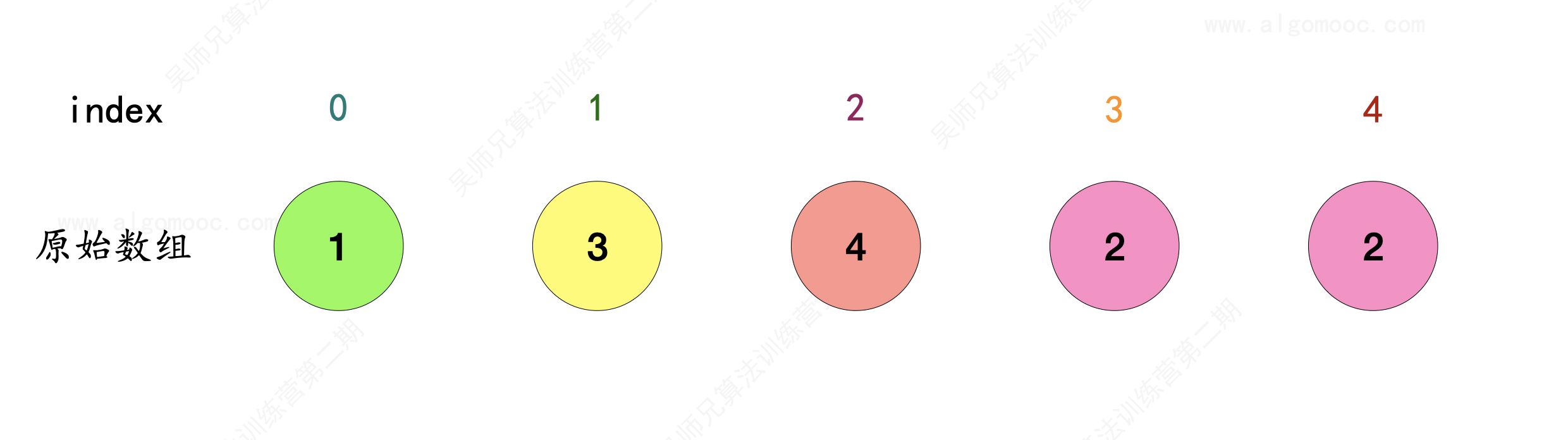
2、比如先选 index = 0 作为链表的起始位置,那么 index = 0 在原始数组 nums 中的对象是 1 ,因此 0 –> 1 。
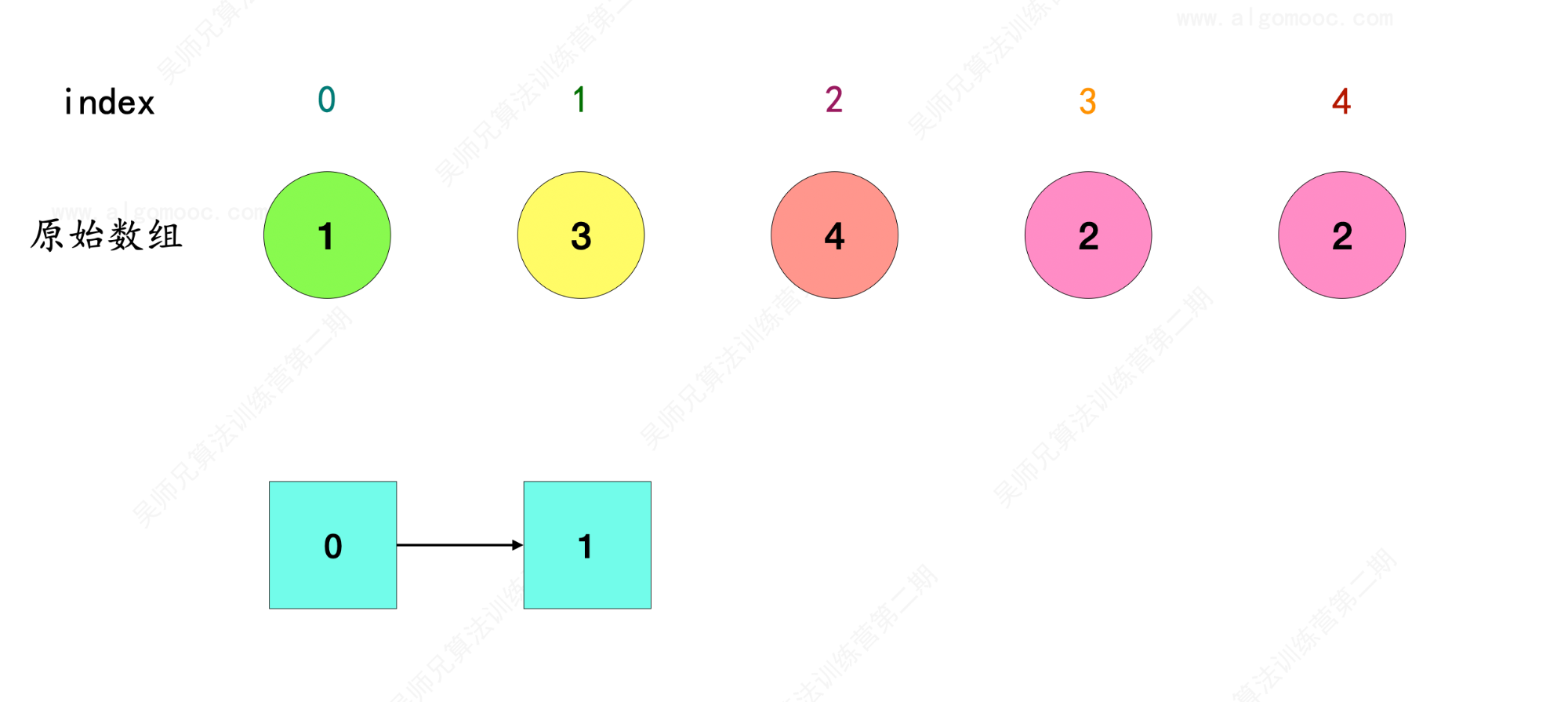
3、index = 1 在原始数组 nums 中的对象是 3 ,因此 1 –> 3 ,和前面串联起来就是 0 –> 1 –> 3 。
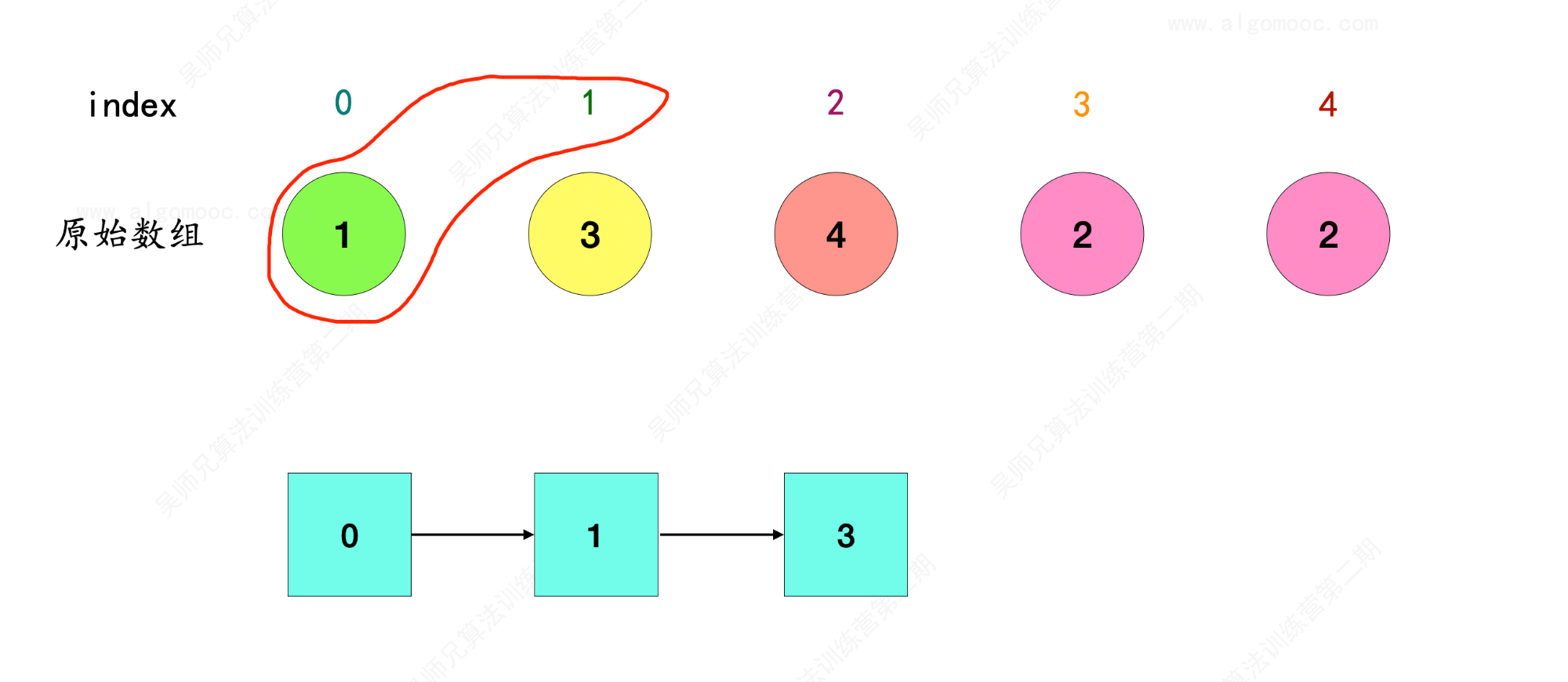
4、index = 3 在原始数组 nums 中的对象是 2 ,因此 3 –> 2 ,和前面串联起来就是 0 –> 1 –> 3 –> 2 。
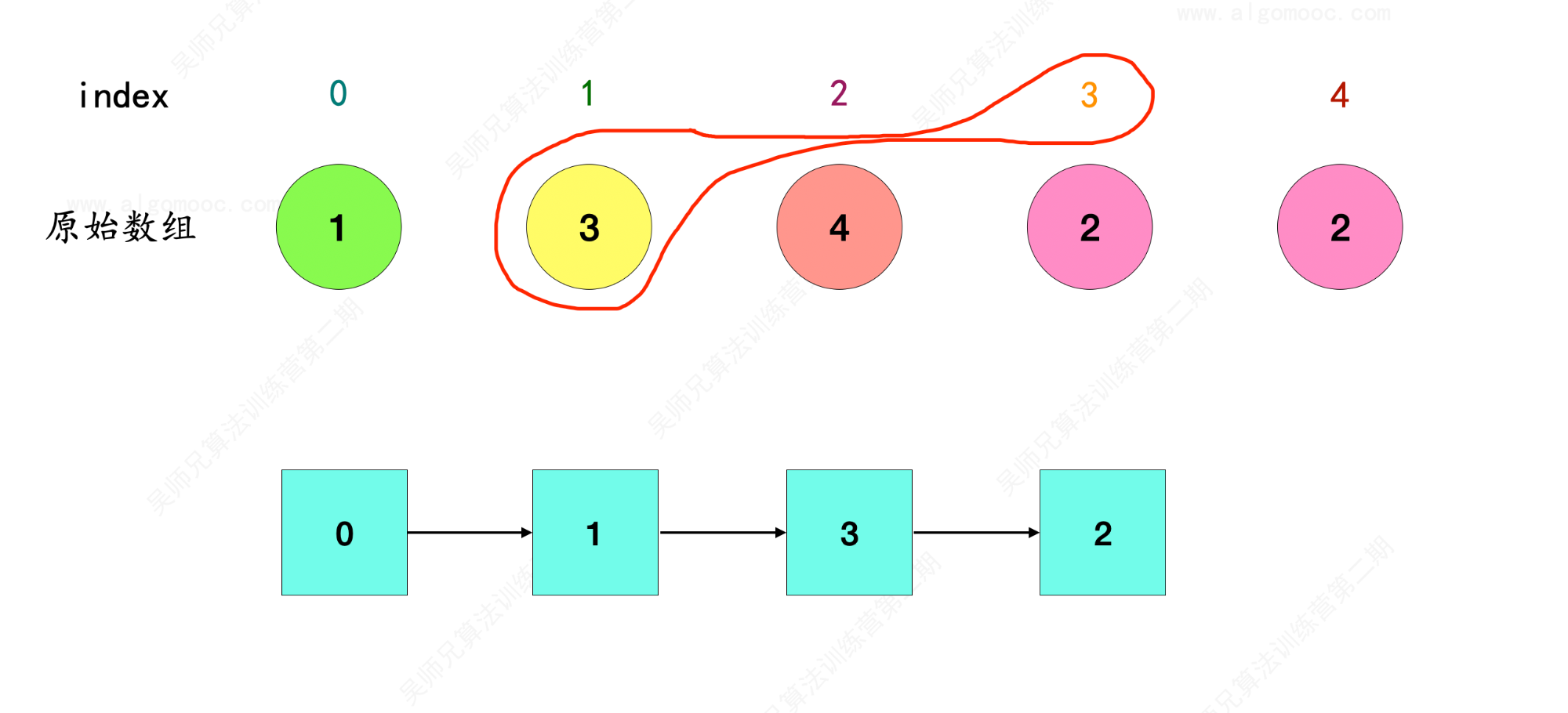
5、index = 2 在原始数组 nums 中的对象是 4 ,因此 2 –> 4 ,和前面串联起来就是 0 –> 1 –> 3 –> 2 –> 4 。
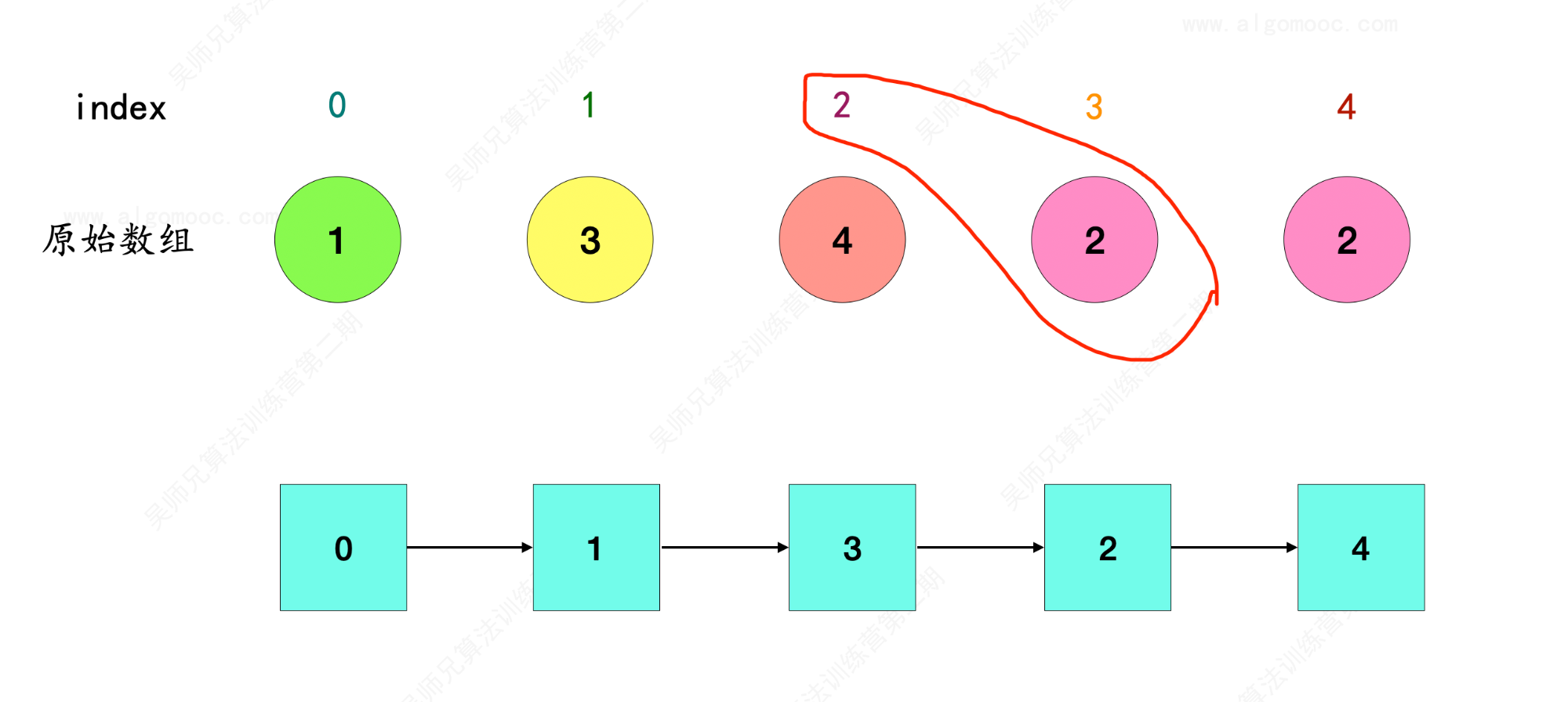
6、index = 4 在原始数组 nums 中的对象是 2 ,因此 4 –> 2 ,和前面串联起来就是 0 –> 1 –> 3 –> 2 –> 4 –> 2 。
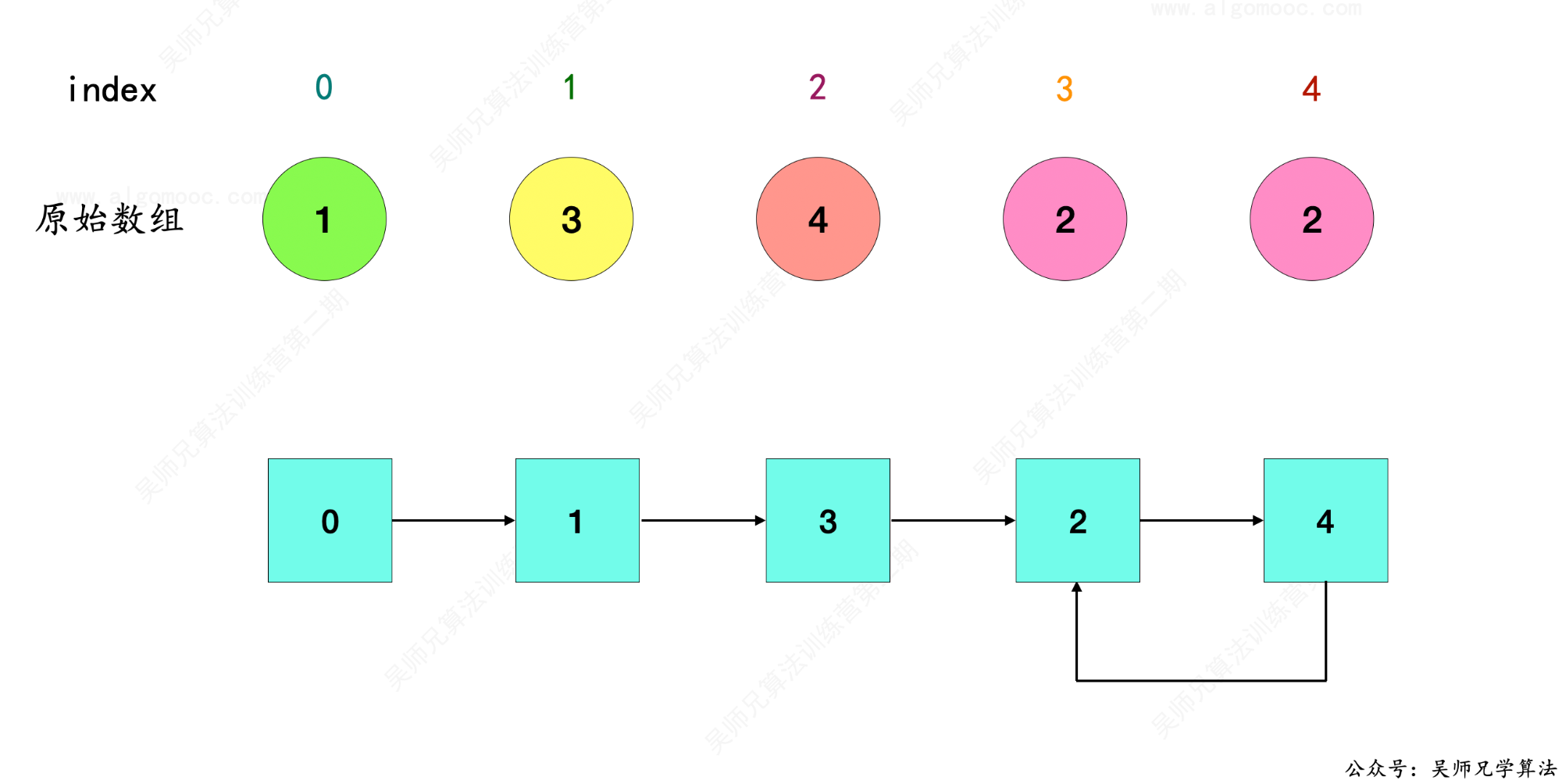
7、在上述的图中,链表中出现了一个环,因为 index = 3 和 index = 4 的对象 nums[3] 和 nums[4] 都等于 2。
8、链表中环的入口就是那个重复的数,那么这道题目也就变成了寻找环入口的题目。
那就和 LeetCode 第 142 号问题:环形链表II 的解法一模一样了。
1、通过快慢指针的方式,在环中寻找它们的第一次相遇的节点位置
2、当快慢指针相遇的时候:
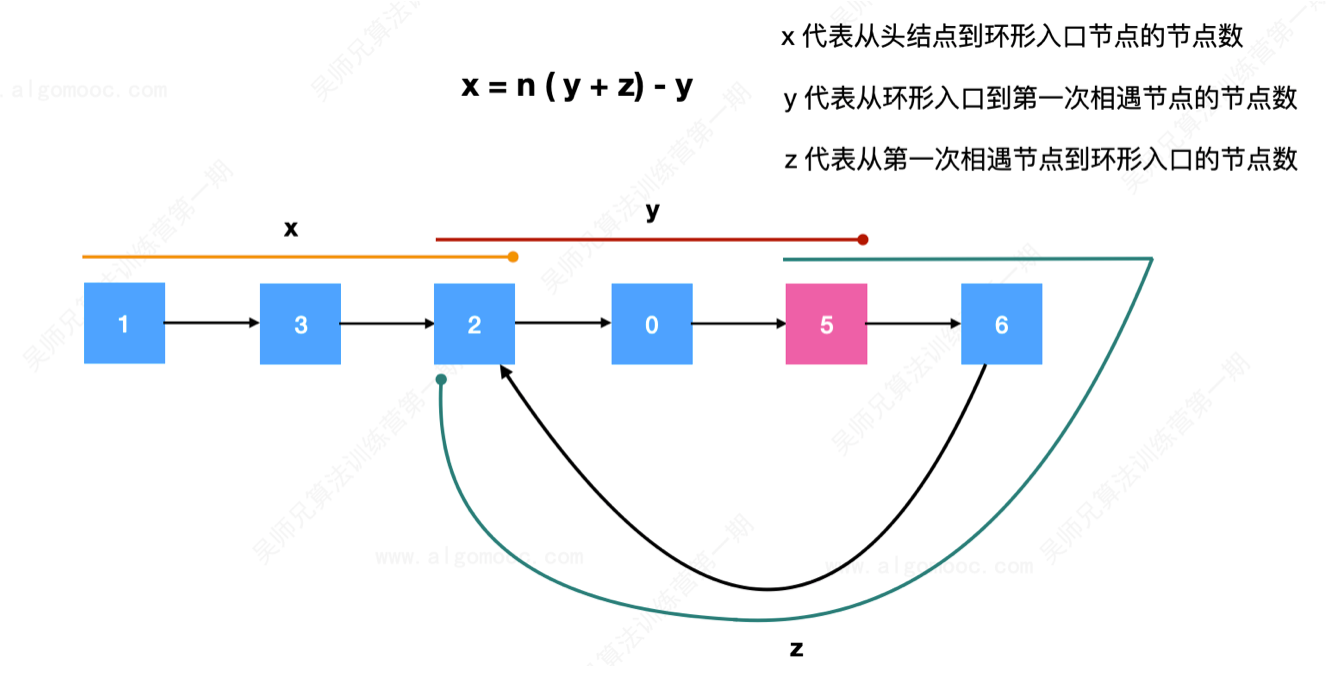
x 代表从头节点到环形入口节点的节点数(不包含头节点)
y 代表从环形入口到第一次相遇节点的节点数(不包含环形入口节点)
z 代表从第一次相遇节点到环形入口的节点数(不包含第一次相遇节点)
此时,快指针走了 x + y + n (y + z),其中,x + y 表示快指针第一次到达相遇节点,n 代表快指针在环里面绕了多少圈。
而慢指针走了 x + y 步。
那么就出现了一个等式 x + y = [x + y + n (y + z)] / 2,即x = n(y + z)- y。
n(y + z)- y 代表的含义是一个指针从相遇节点开始出发,走了 n 圈之后回到原来的出发位置,往后退 y 步。
由于 x 代表从头节点到环形入口节点的节点数,并且x = n(y + z)- y,所以n(y + z)- y 代表的含义就是一个指针从相遇节点开始出发,走了 n 圈之后回到原来的出发位置,往后退 y 步来到了环的入口位置。
那么,我们就可以设置两个指针,一个从链表的头节点开始出发,一个指针从相遇节点开始出发,当它们相遇的时候,代表着环的入口节点找到了。
代码如下:
class Solution {
public int findDuplicate(int[] nums) {
// 1、通过快慢指针的方式,在环中寻找它们的第一次相遇的节点位置
// 2、定义一个慢指针,每次只会向前移动 1 步
int slow = 0;
slow = nums[slow];
// 3、定义一个快指针,每次只会向前移动 2 步
int fast = 0;
fast = nums[nums[fast]];
// 4、如果链表有环,那么无论怎么移动,fast 指向的节点都是有值的
while (slow != fast) {
// 慢指针每次只会向前移动 1 步
slow = nums[slow];
// 快指针每次只会向前移动 2 步
fast = nums[nums[fast]];
}
// 快慢指针相遇,说明有环
// x 代表从头节点到环形入口节点的节点数(不包含头节点)
// y 代表从环形入口到第一次相遇节点的节点数(不包含环形入口节点)
// z 代表从第一次相遇节点到环形入口的节点数(不包含第一次相遇节点)
// y + z 代表环的节点总数
// 此时,快指针走了 x + y + n (y + z)
// 其中,x + y 表示快指针第一次到达相遇节点,n 代表快指针在环里面绕了多少圈
// 此时,慢指针走了 x + y 步
// 由于快指针每次走 2 步,所以快慢指针第一次相遇的时候出现一个等式
// x + y = [x + y + n (y + z)] / 2
// 即 2 * (x + y) = x + y + n (y + z)
// 即 x + y = n(y + z)
// 即 x = n(y + z)- y
// 我们的目的就是去求 x
// 定义两个指针,一个指向相遇节点,定义为 b,一个指向链表头节点,定义为 a
// b 在环中绕圈圈,走了 n(y + z)步会回到原处,即回到相遇节点处
// 由于 y 代表从环形入口到第一次相遇节点的节点数(不包含环形入口节点)
// 所以 n(y + z) - y 时,b 到达了环形入口节点位置
// 由于 x 代表从头节点到环形入口节点的节点数(不包含头节点)
// 所以 a 走了 x 步时,a 到达了环形入口节点位置
// 当 x = n(y + z)- y 时,找到了环形入口节点位置
// 5、开始寻找环入口
// 定义两个指针,一个指向相遇节点,定义为 b,一个指向链表头节点,定义为 a
// 一个指向相遇节点,定义为 b
int b = fast;
// 一个指向链表头节点,定义为 a
int a = 0;
// 让 a 、b 两个指针向前移动,每次移动一步,直到相遇位置
// 由于有环,必然相遇
// 当 b 走了 n(y + z) - y 时,b 到达了环形入口节点位置
// 当 a 走了 x 步时,a 到达了环形入口节点位置
// a 与 b 相遇
while (a != b) {
// a 指针每次只会向前移动 1 步
a = nums[a];
// b 指针每次只会向前移动 1 步
b = nums[b];
}
// 6、返回 a 和 b 相遇的节点位置就是环形入口节点位置
return a;
}
}此时,时间复杂度来到了神奇的 O(n) 级别!
对比之前的二分查找解法,时间复杂度发生了质的变化。
太神奇了!





